Zeros of Polynomial Functions

REMAINDER THEOREM

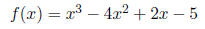
If f(x) is divided by (x - c), then the remainder is f(c).

What is the remainder when f(x) is divided by (x - 3)??

FACTOR THEOREM

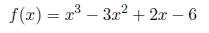
(x - c) is a factor of f if and only if f(c) = 0
Is (x - 3) a factor of f(x)?

NUMBER OF ZEROS

A polynomial function cannot have more zeros than its degree.

RATIONAL ZEROS

Example: Factor 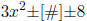and examine the possibilities:

RATIONAL ZEROS THEOREM: Let f be a polynomial function of degree ≥ 1 with integer coefficients.
If p/q (in lowest terms) is a rational zero of f, then p is a factor of a₀ and q is a factor of a_n.

Example: What are the possible rational zeros for

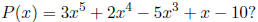
(Note: None of the rational possibilities for this example work -> teaching moment!)

Putting it all together:
Finding zeros of polynomial functions, or solving polynomial equations, will involve the following logical
process:

1. Form a list of possible rational zeros.

2. Graph the polynomial and examine the x-intercepts to choose which of the rational possibilities to
test.

3. Use division to verify the zero.

 •Use the zero value directly with synthetic division.
 •With long division, form the related linear factor with integer coefficients first.

4. Repeat the process, using the depressed polynomial (quotient from the previous division), until the
quotient is quadratic.

5. Find the last 2 zeros from the quadratic polynomial.

You should then be able to write the results either as a list of zeros or as the polynomial in factored form.

Examples:

1. Find the real zeros of f(x) = 2x^3 + 11x^2 - 7x - 6 and write f(x) in factored form.

2. Solve the equation: x^4 + 2x^3 - 7x^2 - 16x - 8 = 0

3. Find the real zeros for f(x) = 2x^4 + 27x^3 + 71x^2 - 94x - 120

4. Find the real zeros for f(x) = 3x^4 + 29x^3 + 57x^2 + 41x + 10

3.5 Assignment: Note the directions.

 •#33, 37, 42. List the potential rational zeros. Stop. we are not using Descartes Rule of Signs
 •#46, 55. Use the rational zeros to find all the real zeros of the function. Stop.
 •#59, 62. Solve the equation in the real number system. Stop.
 •#105. Hint: The Remainder Theorem really says two things are equivalent.

FUNDAMENTAL THEOREM OF ALGEBRA | A REALLY BIG DEAL (for us mathematicians)!!!

Every complex polynomial function f(x) of degree n≥1 has at least one complex zero.

Extensions (probably more meaningful to students, and definitely more practical!)

1. Every complex polynomial function f(x) of degree n≥1 can be factored into n linear factors (not
necessarily distinct).

2. Every complex polynomial function f(x) of degree n≥1 has n zeros.

3. Complex zeros occur in conjugate pairs. (If a + bi is a zero, so is a - bi).

4. Every odd degree polynomial has at least 1 real zero.

Examples:

1. Given zeros of -1, 3, 2i, find a polynomial function f(x).

2. If (2 + i) is a zero of f(x) = x^4 - 8x^3 + 64x - 105, find the remaining zeros.

3. Find all the zeros of f(x) = 3x^4 + 5x^3 + 25x^2 + 45x - 18