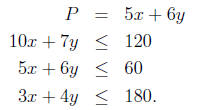Sample Problems for Math 111 Test 1 Solutions

16. Use any method you like to find the point of intersection of the lines
2x + 5y = −1 and 3x + y = −8.
Solution: One option is to solve the second equation for y, to get
y = −3x − 8.
Substituting this into the first equation we have

2x + 5(−3x − 8) = −1
2x − 15x − 40 = −1
−13x = −1 + 40	adding 40 to both sides
−13x = 39
x = −3.

Substituting x = −3 in the first equation we have
2(−3) + 5y = −1.

Solving this we have y = 1. Thus the solution is x = −3 and y = 1. We
can check the answer with the second equation to see that this solution
is correct.
A second method would be to use matrices.

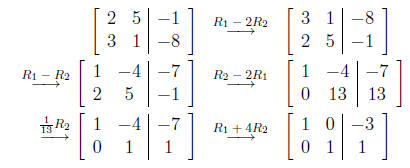
This gives us x = −3 and y = 1.
Of course, if you have a calculator, you could set this one up with
the calculator. However, you might have to solve a 2 × 2 on the no
calculator/study sheet allowed portion.
The third method would be elimination. To find the y value we would
multiply the first equation by 3, the second equation by 2, and then
subtract to obtain:
13y = 13

and thus y = 1. We could either substitute in for y or multiply the
second equation by 5 and subtract the first equation from it to obtain
13x = −39

or x = −3, and again the solution is x = −3 and y = 1.

17. Consider the system
2x − 4y = −6
−3x + 6y = k.

For what values of k does the system have
(a) no solutions?
(b) exactly one solution?
(c) infinitely many solutions?

The easiest way to solve this is to first simplify the first equation by
dividing both sides by 2. We have that the equations are
x − 2y = −3
−3x + 6y = k

Note that if we now multiply the first equation by −3 we get
−3x + 6y = 9
−3x + 6y = k

The only way that we can have any solutions is if k = 9, but in that
case there would be infinitely many solutions. Hence:
(a) There are no solutions is k ≠ 9.
(b) There is no value for k which gives exactly 1 solution.
(c) There are infinitely many solutions if k = 9.

18. Write the augmented matrix for the system
2x − z = 1
3x + 2y = 4.

Be careful!!
Solution:

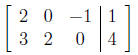
19. For what values of k, m, and n is 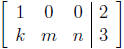in row reduced form?
Solution: To have row reduced form, we need to have either k = 0,
m = 1, and n can be anything, or k = 0, m = 0, and n = 1.
The requirement is that each row should have a leading 1 and that any
column with a leading 1 should have 0s elsewhere. This means that
k = 0 since it is below a leading 1. Since row two must have a leading
1, then m = 1 or m = 0 and n = 1. Now if m = 1, then n can be
anything since it will not be in a column with a leading 1.

20. Use the indicated row operations to fill in the 5 missing entries in the
second matrix below:

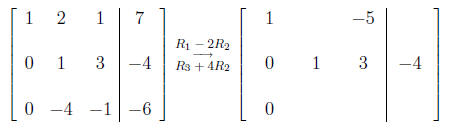
Solution: The matrix should be:

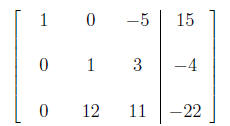
21. (a) Write down the augmented matrix for

x − z = −2
y + 2z = 7
−x + 2z = 6.

Solution: The matrix would be

(b) Write down what operation should be the first row operation to
undertake in Gauss-Jordan elimination.
Solution: The first row operation should be R₃ + R₁. This would
make the entry in the 3, 1 position a 0.

22. Sandy has a total of $3,500 on deposit with two savings institutions.
One pays interest at the rate of 6% per year and the other pays interest
at the rate of 7% per year. If Sandy earned a total of $250 in interest
during a single year, how much does she have on deposit in each institution?

Solution: There was an error in this problem. The question should
have read that the interest paid was $220 not $250. Below I will solve
the problem with $250, and you will see why there must have been an
error. Then I will give the solution with 220 instead.
We will let x denote the amount of money in the first institution (paying
6%) and y denote the amount of money in the second institution
(paying 7%). Since her total is 3500 we have the equation

x + y = 3500.

That the interest paid was 250 dollars, gives the equation
.06x + .07y = 250.

Thus we have the equations
x + y = 3500
.06 + .07y = 250

This gives us the augmented matrix

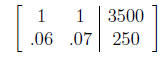
Row reducing this on our calculator yields the matrix

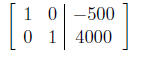
This matrix corresponds to Sandy investing −500 dollars in the account
paying 6% interest, which is ludicrous. Hence we know that the problem
(or our solution) must have an error.
Note: For this problem, it really is that problem that has the error,
but if it was a solution error that you didn’t have time to fix (i.e., if
you see this happen on a test) you should tell me that you know the
answer is wrong and why. Checking your answer and discovering it is
wrong is worthwhile, and I take off fewer points for an incorrect answer
that you can explain why you know it is wrong.
Now for the correct problem, the initial matrix should be

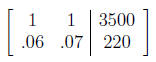
Row reducing this matrix yields

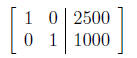
This corresponds to the equations x = 2500 and y = 1000. Thus there
must be $2500 invested in the first institution and $1000 invested in
the second.

23. Below is a row-reduced matrix. Write down the system of equations
corresponding to this matrix, and then write the solution for the corresponding
equations using the parameter t.

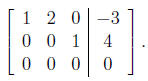
Solution: The equations corresponding to the matrix are

x + 2y = −3
z = 4

Since there is no leading one in the second column, we will begin by
setting
y = t.
Now solving for the other two equations we have the solutions are
x = −3 − 2t
y = t
z = 4.

24. If 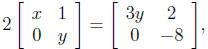find x and y.

Solution: Using the matrix operations, we have

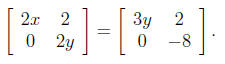
Setting the terms equal to each other, we have
2x = 3y
2y = −8

The second equation implies that y = −4. Substituting into the first
equation we have x = −6.

25. Write down the corresponding matrix equation to the system of linear
equations below, and solve it (via calculator) using the inverse matrix
(show the inverse matrix):
2x + 3y + 4z = 12
x − 5y + 2z = 4
3x − y + z = 1

Solution: In matrix form, this is

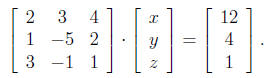
To solve, we enter the matrix (call it A) in our calculator to obtain

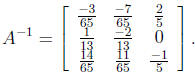
Multiplying the solution column vector by this matrix gives solution:

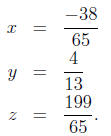
26. A T-shirt company wants to manufacture 2 types of T-shirts. The first
T-shirt requires 10 minutes on machine A, 5 minutes on machine B,
and 3 minutes on machine C. The second T-shirt requires 7 minutes
of manufacturing time on machine A, 6 minutes of manufacturing time
on machine B, and 4 minutes of manufacturing time on machine C.
The first T-shirt sells for a profit of 5 dollars and the second T-shirt
sells for a profit of 6 dollars. Set up the linear programming problem
for this company. Label all of your variables.
Correction to question: Oops, I didn’t include the amount of time
on each machine... sorry. Suppose machine A has 2 hours available,
machine B has 1 hour available, and machine C has 3 hours available.
Solution: Let x denote the number of the first T-shirt to be made,
and y denote the number of the second T-shirt to be made. For the
requirements on machine A, we know
10x + 7y

For machine B we have 5x + 6y and for machine C, we have 3x + 4y.
Of course since there aren’t any negative numbers of T-shirts, x≥0
and y≥0. We are trying to maximize the profit function P = 5x+6y.
Thus the final set of equations is: