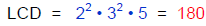LEAST COMMON MULTIPLE/LEAST COMMON DENOMINATOR
The least common multiple (LCM) of a given set of
numbers is the smallest positive number divisible
by the numbers in the set. For example, if we list the multiples of 4 and 6, we
can see these numbers
share common multiples of 12, 24, 36, and 48 to name a few.
Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44,
48, …
Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, …
Even though 24, 36 and 48 are multiples of 4 and 6, the
LCM is 12 because 12 is the smallest number
divisible by 4 and 6.
When we need to find a common denominator for a given set
of fractions, the LCM is called the least
common denominator (LCD). To find the LCD of a given set of fractions, check
the denominators of
the fractions:
STRATEGIES
1) Do the smaller denominators divide the larger? If they do, the larger denominator is the LCD.
EXAMPLE 1: Find the LCD of
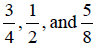
Because 8 is divisible by 4 and 2, the LCD = 8.
2) Are the denominators prime or relatively prime numbers?
(Prime numbers are numbers divisible
only by themselves and 1; relatively prime numbers share no common factor.) When
the
denominators are prime or relatively prime, multiply the denominators to find
the LCD.
EXAMPLE 2: Find the LCD of
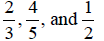
The denominators of the fractions are prime numbers. To find the LCD, multiply the denominators:
LCD = 2 3 5 = 30.
EXAMPLE 3: Find the LCD of
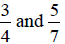
The denominators of the fractions are relatively prime
numbers because they share no common
factors: 4 = 2*2 and 7 = 1*7. To find the LCD, multiply the denominators:
LCD = 4*7 = 28.
EXAMPLE 4: Find the LCD of
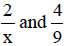
Because the value of "x" is unknown, the only factors of x
are "1" and "x." This means that 9 and
"x" share no common factors, so the LCD = 9 x.
3) If the largest denominator is not divisible by the
smaller denominators, list the multiples of the
largest to find the LCD.
EXAMPLE 5: Find the LCD of
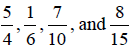
The smaller denominators do not divide the larger. As
shown below, we find the LCD sooner when
we list the multiples of the largest denominator.
Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44,
48, 52, 56, 60, …
Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 64, 60, …
Multiples of 10: 10, 20, 30, 40, 50, 60, …
Multiples of 15: 15, 30, 45, 60, …
LCD = 60
4) If the LCD is not among the first 5 or 6 multiples you list, try prime factorization and a factor box.
EXAMPLE 6: Find the LCD of
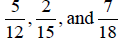
Step 1: Write the prime factorization of each
denominator and list the factors in a table of primes,
as shown:
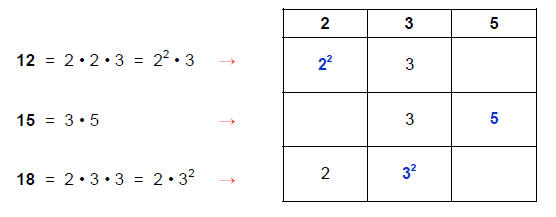
Step 2: Take the highest power of any factor the
numbers share in common and any factor the
numbers do not share in common. The LCD is the product of these factors: