Flow

Written mathematics must be readable. This may seem trivial, but it is an important point. You
should be able to read your work aloud to a classmate and have them understand your solution. If
you need to add any explanations, these should be included in your written work. The most common
mistake is to write mathematics without using enough words. All writing, even mathematics, should
consist of complete sentences. These should explain the problem by providing both the method and
justification for each step of the solution.

Why are sentences important in mathematics?

Although sometimes it seems hard to read textbooks, it would be much harder to understand if
they only had equations and no sentences. The situation is similar in lecture: if the professor just
listed formulas on the chalkboard without talking about them, leaving you to figure out what was
being done in each step, how much could you understand from the lecture? Neither of these would
be a good way for most students to learn, since sentences are necessary to explain the mathematics.

Why should students use sentences in a Mathematics class?

In a Mathematics class, you should explain homework solutions using complete sentences. That
means linking together thoughts with words and embedding equations into sentences. Going through
the extra work to do this will benefit you in several ways:

• Writing down your thoughts and organizing them into complete sentences will help you to
understand the method of solution better.

• When you look back on homework to study for a test, or later on in another class, you will
understand what you were doing on each problem and the mathematics behind it.

• Other people (teacher, classmates, grader,...) will understand what you are doing at each step,
and why you are doing it. This way, you won’t lose points for skipping steps or solving the
problem in an unusual way.

• Communicating your work will be essential in whatever field you choose. Even though the
fields are stereotypically weak on writing, engineers and scientists spend a surprising amount
of time writing reports and giving oral presentations.

Examples:

How to put an equation into a sentence:
Good: The derivative of the curve
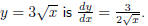
Bad: The derivative 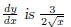for the curve y which is
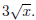
Bad: 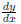is the derivative of 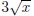which is .

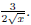Using sentences incorrectly:

Find an equation for the tangent to the curve 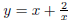at the point (1, 3).
Bad:

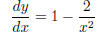
so the equation for the derivative is

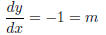
so the slope at (x, y) can be found by y −3 = −1(x−1) so y = −x+4 is the point-slope equation.

Good:
We first check that (1, 3) is a point on the curve by plugging these values in: 3 = 1 + 2/1. The
derivative of the curve 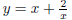is

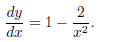(1)

A line tangent to the curve at the point (1, 3) will have slope

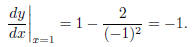
Using the point-slope formula with m = −1, x₀ = 1, and y₀ = 3 gives the formula for the line
y − 3 = −1(x − 1). Solving for y and simplifying gives

y = −x + 4.

This is the equation of the line tangent to the curve at that point.

Vague and uninformative sentences

Bad: We use calculus to find that y = 3x² + 1 has a slope of 3 at x = 1/2.
Good: To find the slope of the curve y = 3x²+1 at the point x = 1/2 we find 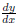evaluated at x = 1/2.

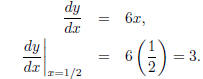
Bad:

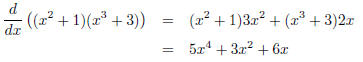
is the derivative.

Good: To take the derivative of a product of 2 functions, we use the product rule, (fg)' = f'g + fg'.
In our case we have

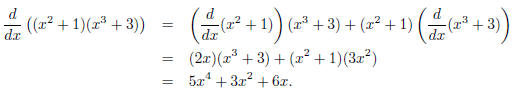
Referring to previous equations and figures.

You may have noticed that one of the equations above has been labeled equation number one by
putting “(1)” at the right hand margin. If you need to refer back to an equation or figure, label it
and then refer to it by its label. Do not draw arrows.

Bad: Using the equation from before, the slope is −1. Which equation?
Good: Using (1), the derivative at x = 1 is −1.