Prime factorization, Greatest Common Factor, and Least Common Multiple
1.1 Factoring
Factoring is the act of breaking an object into its smallest parts. In
Mathematics, we call
the smallest parts prime.
1.1.1 Definition
A factor of a given number is the same as a divisor, that is, a number that
divides evenly
into the given number. We say that a number is divisble by all its factors.
1.1.2 Definition
A prime number is a number whose only factors are 1 and itself. To avoid
confusion, we
do not consider 1 to be a prime number, as its only factor is itself.
1.1.3 Example
The factors of 12 are: 1, 2, 3, 4, 6, and 12. The prime factors of 12 are: 2 and
3.
Sometimes we like to factor a number into it Prime Factorization. When we do
this
we are looking for all occurrences of primes as factors of a given number.
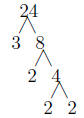
1.1.4 Example
The prime factorization of 24 is: 24 = 23 · 3. We can get this by making a factor
tree:
The following are some tricks to determine what numbers are factors of a
given number:
• If the number is even, that is, if it ends in a 0, 2, 4, 6, or 8, then it is
divisible by 2.
• If the sum of the digits of a given number is divisible by 3, then so is the
given number.
• If the number ends in a 0 or 5, then it is divisible by 5.
• If the sum of the digits of a given number is divisble by 9, then so is the
given number.
• If the number ends in a 0, then it is divisble by 10.
• If the number is less than 100 and has the same digit twice, then it is
divisble by 11.
1.1.5 Example
1. 1024 is divisible by 2, because it is even.
2. 237 is divisible by 3, because 2+3+7=12 and 1+2=3 so 12 is divisble by 3 and,
therefore,
so is 237.
3. 345 is divisble by 5, since it ends in a 5.
4. 123456789 is divible by 9, because 1+2+3+4+5+6+7+8+9=45 and 4+5=9 so 45 is
divisible by 9 and, therefore, so is 123456789.
5. 470 is divisible by 10, because it ends in a 0.
6. 55 is divisble by 11, since both digits are the same.
1.2 Greatest Common Factor
1.2.1 Definition
The greatest common factor for a group of number is the largest number that
divides
evenly into all numbers in the group.
1.2.2 Example
Find the greatest common factor (gcf) for the following group of numbers: 12,
40, 64.
Solution: First we should make a factor tree for each of the above numbers:
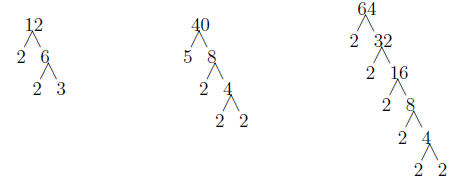
So 12 = 22 · 3, 40 = 23 · 5, and 64 = 26. So
we can see that every factorization has a 22 in
it and that is the largest in all three. So the gcf= 22 = 4. Notice
we used the smallest power
for each of the primes. If we used 23, instead, we would not get that
the gcf divides into 12.
1.3 Least Common Multiple
1.3.1 Definition
A multiple of a given number is a number that the given number divides evenly
into. That
is, a number is a factor of all its multiples.
1.3.2 Definition
The Least Common Multiple for a group of numbers is the smallest number that is
a
multiple of every number in the group.
1.3.3 Example
Find the Least Common Multiple (LCM) of the following numbers: 12, 32, 30.
Solution: First we must find the prime factorization of each of the given
numbers:
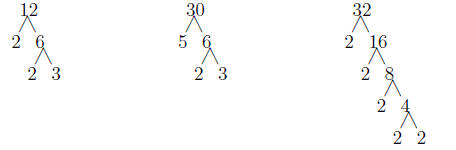
So, 12 = 22 · 3, 30 = 2 · 3 · 5, and 32 = 25. So The
LCM=25 · 3 · 5 = 480. Notice we
needed the highest power for each prime. If we used 24, instead, then
we wouldn’t get that
32 divides into the LCM.
Section 1 Exercises
Directions: Factor the following numbers into their prime factorization:

Directions: Find the Greatest Common Factor and the Least Common
Multiple of each group
of numbers:
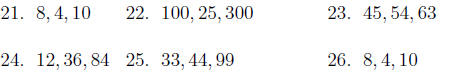
2 Order of Operations
In mathematics there is a certain understood order in which an expression can
be simplified.
This order is called order of operations. Many remember the order of operations
by
memorizing a meaningless word: PEMDAS. As I said, this word really has no
meaning except
that it is an acronym for Parenthesis, Exponents, Multiplication, Division,
Addition, and
Subtraction. This is the order in which one should simplify any expression.
2.0.4 Example
Simplify: 3(4 − 2)
We should do what is in parenthesis first then we multiply:
3(4 − 2) = 3(2) = 6
Let’s try some that are a little harder
2.0.5 Example
Simplify: 2 − 2[(5 − 6)3 + 7 · 4]
For this we need to first go inside the square brackets, then inside there start
over on the
order of operations and go inside the parenthesis to get:
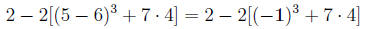
Then we need to do the exponent (still inside the square brackets)
= 2 − 2[−1 + 7 · 4]
Now we need to do the multiplication inside the square brackets:
= 2 − 2[−1 + 28]
Now we can add inside the brackets:
= 2 − 2[27]
Next we do the multiplication:
= 2 − 54
Finally, we can subtract:
= −52
Let’s do one more:
2.0.6 Example
Simplify:
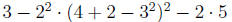
We will again follow the order of operations to get the value of this expression:
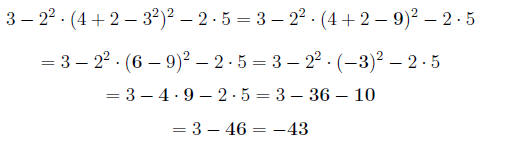
Section 2 Exercises Directions: Simplify each expression using order of operations:
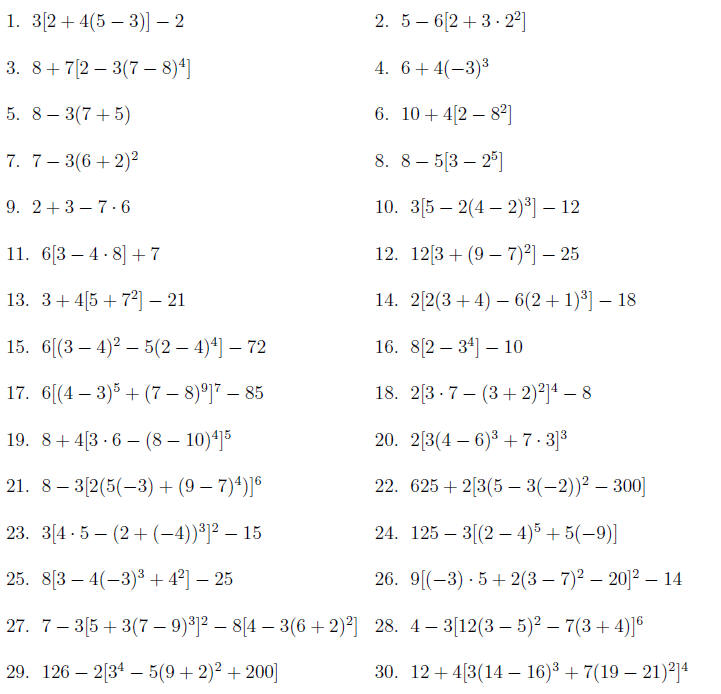
3 Fractions
3.1 Reducing fractions
A fraction is in reduced form if the GCD of the numerator and the denominator is
1, that
is, if the numerator and denominator have no common prime factors.
To get a fraction into reduced form we must factor the numerator and denominator
in to
their prime factorization and cancel the like factors:
3.1.1 Example
Reduce: 3/6
The numerator is already written as its prime factorization as 3 is prime. The
denominator
can be written as 6 = 2 · 3. So we rewrite the fraction as:
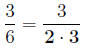
Now we can cancel a 3 from the top and bottom to get:
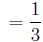
3.1.2 Example
Reduce: 36/60
First we should factor the top and bottom to get:
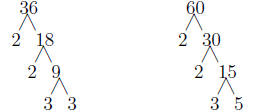
So we can rewrite the fraction as:

3.2 Adding and Subtracting Fractions
When adding and subtracting fractions we need to get a commond denominator. A
common
denominator is a the LCM of all the other denominators.
3.2.1 Example
Find the common denominator for the fractions:
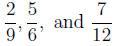
So we need to find the LCM of 9, 6, 12. So we do as we did in 1.1.3 to get
the common
denominator=36.
3.2.2 Example
Add:
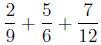
From Example 1.3.1 we have that the common denominator is 36. So we need to
make
all of our denominators 36. We do this by multiplying the numerator and
denominator of
each fraction by the appropriate number:
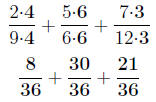
Now we can just add the tops:
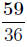
Let’s try another a bit more difficult:
3.2.3 Example
Find:
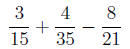
First, we find the commond denominator by factoring each of the denominators:
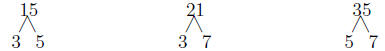
So we have 15 = 3·5, 21 = 3·7, and 35 = 5·7. So the common denominator =
3·5·7 = 105.
So we now multiply by the appropriate numbers on top and bottom to make the
denominators
common:
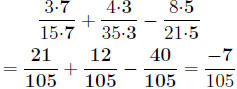
Some may ask why we need a common denominator. The way to think about
fractions
is as parts. The following is an example where fractions may be common in daily
life:
3.2.4 Example
(a.) 5/8 can be thought of as 5 pieces of a large pizza which usually has 8
slices. So if someone
eats half of one large pizza and one-forth of another, then ate
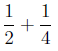
of a pizza. This is 4 slices of one and 2 slices of another which is 6 slices
of pizza. So the
person ate
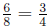 of a pizza.
of a pizza.
3.3 Multiplying and Dividing Fractions
When multiplying fractions it becomes easier to reduce first and then
multiply the numerators
and multiply the denominators.
3.3.1 Example
Multipy:
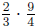
We can rewrite by factoring the numerators and denominators:
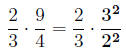
Now we can cancel any factors that are common to both the top and the bottom.
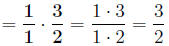
Let’s do a more difficult example:
3.3.2 Example
Multiply:
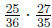
We can begin by factoring the numerators and denominators to get:
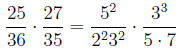
Now just cancel factors that are common to both the top and bottom:
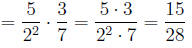
When dividing fractions we should first invert the second fraction and then
multiply
them.
3.3.3 Example
Divide:
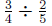
First, we invert the second fraction to get:
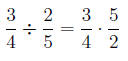
Now we do as we did above to multiply:
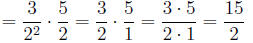
One more example:
3.3.4 Example
Divide:
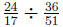
We’ll invert and then multiply:
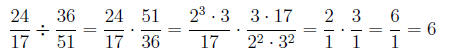
Section 3 Exercises
Directions: Add or subtract. Reduce your fraction to lowest terms.

Directions: Multiply or divide and write your answer in reduced form.
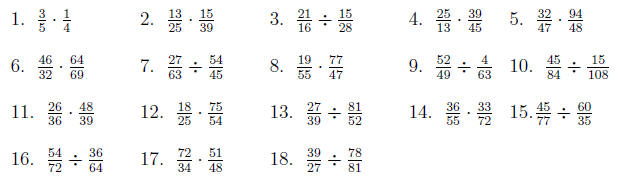
4 Complex Fractions
4.0.5 Definition
A complex fraction is a fraction with fractions in the numerator and/or the
denominator.
4.0.6 example
An example of a complex fraction is:
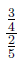
There are different ways to simplify a complex fraction:
1. Simplify the top into one fraction and then simplify the bottom into one
fraction and
then divide the fractions.
2. Find a common denominator that is common to all fractions both on top and on
bottom and then multiply the top and bottom by them.
4.0.7 example
Here we will simplify the complex fraction:
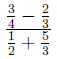
using both methods.
1.
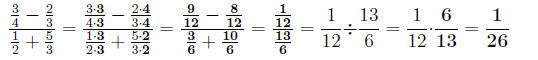
2. Notice the common denominator for all the fractions is 12
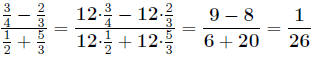
Either way is valid. I tend to like the second way. It turns the complex
fraction into a
regular fraction in one step.
4.0.8 Example
One more example, this time I’ll just use the second method: Simplify:
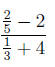
Notice the common denominator is 15:
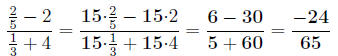
Section 4 exercises Directions: Simplify the complex fractions:

5 Absolute Value
5.1 Numbers
5.1.1 Definition
The Absolute Value of a number is the distance the number is from zero, we
denote it |a|.
Mathematically, we have:
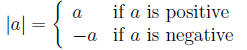
5.1.2 Remark
This is the same as making sure the result is positive.
5.1.3 example
Find the absolute value of the following:
1. |2|
solution If we look at a number line, we have:
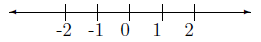
Notice the number 2 is two numbers away from zero so |2| = 2. Of course, the
easiest
way to do this is to say, 2 is positive, so |2| = 2
2. | − 2|
solution For this one we can again look at the above number line and see that −2
is
two numbers away from zero, so |−2| = 2. And the easier way to do this is to
just say
that -2 is negative so we make it positive with the absolute value and we get:
|−2| = 2
We can make the examples a little harder:
5.1.4 example
Find | − (−(−(−4)))|
solution Remember all absolute value does is make things positive. So it doesn’t
matter
how many negative signs there are, absolute value will always ignore them all.
So, we get:
| − (−(−(−4)))| = 4
5.2 Distance between two numbers
We can also use absolute value to find the distance between two numbers.
5.2.1 Definition
The distance between two numbers, a and b, is |a − b|.
Notice that when we say distance we want something that is positive. If a−b is
negative
then the absolute value takes care of it and makes it positive.
5.2.2 Example
Find the distance between 4 and -8.
solution: The distance between 4 and -8 is |4 − (−8)| = |4 + 8| = |12| = 12.
5.2.3 Example
Let’s make it a little harder: Find the distance between 2 and
π (remember π≈3.14159
. . .)
solution: The distance is |2 − π|, but 2 is smaller
that π so we know 2 − π is
negative.
According to the definition of absolute value we have: |2− π|
= −(2− π) Now we know that
since 2 is smaller than π, we can subtract the other
way (the distance between 2 and π is
the same as the distance between π and 2) to get the
distance is |π − 2| = π − 2
So now
we know two things: (1.) The distance between 2 and π
is π − 2 and (2.) We found that
−(2 − π) = π − 2. We’ll need
that information later.
Section 5 exercises Directions: Evaluate each absolute value expression:

Directions: Find the distance between each pair of numbers:
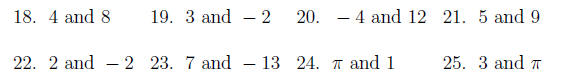
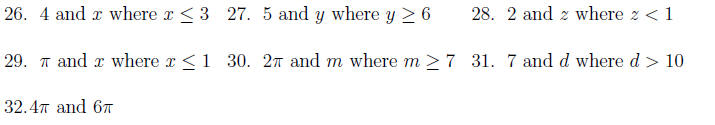
6 Exponents
6.1 The definition and some simple properties
When we learned how to multiply we see that it is a fast way of adding, that is,
for example,
3 · 4 = 4 + 4 + 4 = 12. A similar idea is using exponents to multiply fast.
6.1.1 Definition
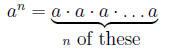
6.1.2 Example
34 = 3 · 3 · 3 · 3 = 81.
Some basic properties one will need are the following:
6.1.3 Basic Properties
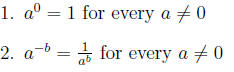
6.1.4 Example
Simplify: 3-2
solution 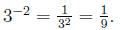
6.1.5 Example
Simplify: 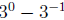
solution 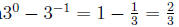
Section 6.1 exercises Directions: Simplify:
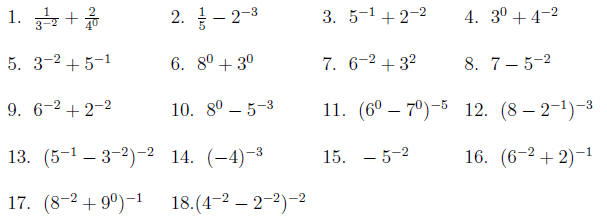
6.2 Expressions
An expression is a mathematical entity that may or may not contain variables. An
expression
can be manipulated, but never solved. We will start by evaluating expressions
and later
we will learn to simplify them and then to use them in equations (which can be
solved).
6.2.1 Example
Evaluate the expression: 3x − 3y, when x = 1, y = −2
Solution 3(1) − 3(−2) = 3 + 6 = 9.
6.2.2 Example
Evaluate the expression:
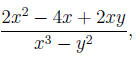 when x = 1, y = −2
when x = 1, y = −2
solution
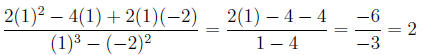
Section 6.2 exercises Directions: Evaluate each expression
given the values for x and y: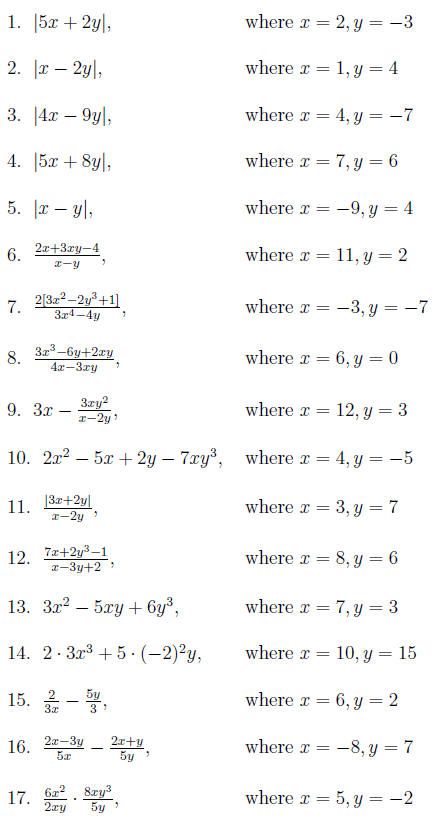
6.3 Exponential Expressions and the Properties of
Exponents
Now that we know the basics about exponents we can learn to simplify exponential
expressions.
6.3.1 Properties
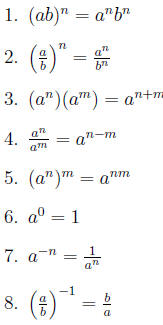
Reasoning for the above properties:

Now the a’s will cancel and leave n −m of them on top or m
− n of them on bottom.
SO we get:
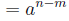
5.
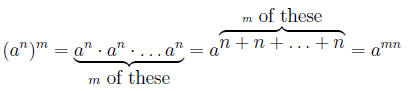
Notice we used # 3 to get the second equality here.
6.
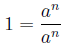
Here we used that anything divided by itself is 1
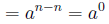
Here we used # 4.
7.
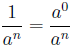
Here we used # 6.
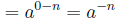
Here we used # 4.
8.
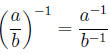
Here we used # 2.
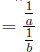
Here we use # 7.
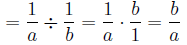
6.3.2 Example
Simplify: 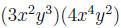
solution 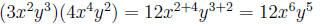
6.3.3 Example
Simplify:
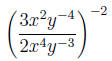
Solution
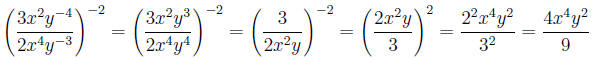
Section 6.3 exercises Directions: Simplify. Your answer
should contain only positive
exponents.: