Significant Figures in Measurements and Computations

Uncertainty in Measurements: The word accuracy has various connotations depending on the
circumstances under which it is used. In the study of physics it is commonly used to denote the
reliability of a number or the limiting accuracy of a measurement.

As applied to a measurement, the accuracy is expressed by stating the uncertainty of the numerical
result, that is, the estimated maximum amount by which the result may differ from the "true" or
accepted value.

For instance, if we have a keg advertised to contain 15,000 nails, we can assume that there are
between 14,000 and 16,000 nails. The uncertainty amounts to +/- 1 in the last significant figure.

Significant Figures: The accuracy of a physical measurement is properly indicated by the number
of figures used to express the numerical measure. Conventionally, only those figures that are
reasonably trustworthy are retained. These are called significant figures.

In recording certain numbers, the location of the decimal point requires zeros to be added to the
significant figures. These zeros serve only to locate the decimal point and are never considered
significant.

Examples:
Length of a page 22.7 cm (3 significant figures)
Thickness of a page = 0.011 cm (2 significant figures)
Distance to the sun = 149,600,000 km (4 significant fig)
Speed of light = 299,790 km/sec (5 significant figures)

If each of these numbers is expressed in terms of scientific notation, there is no doubt as to the
number of significant figures for only the significant figures are then retained. Thus:
Length of page = 2.27 x 10¹ cm
Thickness of a page = 1.1 x 10^-2 cm
Distance to the sun = 1.496 x 10⁸ km
Speed of light = 2.9979 x 10⁵ km/sec

Do not be confused by the placement of a zero in a string of numbers. For instance, say the land
speed record for a bicycle is 80.13 miles per hour. In this case the zero does more than position the
8, 1, and 3. It indicates that the number is 80, not 79 or 81 miles per hour. A zero imbedded in a
string of significant figures can never itself be considered non-significant. The number 80.13 is
accurate to 4 significant figures.

Further, do not be confused by a zero that is said to be of significance. Something may be measured to
an accuracy of 2.000 units. In this case we know that the measurement is accurate to three decimal
places. That is, the measurement lay somewhere between 2.001 and 1.999.

There are some numbers that, by their definition, may be taken to have an unlimited number of
significant figures. For example, the integer 2 and the irrational number ! in the following
relationship for a circle: circumference = 2πr where r is the radius of a circle.

In calculations there is frequent need to use data that have been recorded without a clear indication of
the number of significant figures. For example, a textbook problem may refer to a "two-kilogram
mass", or in an experiment a student may announce that she has measured a certain distance as "3
meters". In such cases the values with the approximate number of significant figures should be written
from what is know or assumed about the way in which the measurement were made. If the distance
referred to were measured with an ordinary tape measure, the distance might appropriately be written
as 3.0 meters. If the distance were carefully measured with a steel scale accurate to the nearest
millimeter, the distance might be recorded as 3.000 meters. In academic problem work a good rule to
follow is to retain three figures unless there is good reason to decide otherwise.

Recapping: The significant figures in a quantity are the meaningful digits in it. There are several
conventions to keep in mind when dealing with significant figures:

1) Any nonzero digit is a significant digit. Examples: 3.14 has three significant digits and 239.67
has five significant digits.
2) Zeros in between nonzero values are significant digits. Example 20.4 has three significant digits.
3) Zeros to the left of the first nonzero digit are NOT significant. Example: 0.0012 has two
significant digits.
4) For numbers with decimal points, zeros to the right of nonzero digits are significant. Example:
Both 2.0 and 0.0020 have two significant digits.
5) For numbers without decimal points, zeros to the right of nonzero digits may or may not be
significant. Example: 350 may have two or three significant digits. To avoid confusion, use a
decimal point: 350. has three significant digits, 350 has two.
6) The last significant digit in a number should have the same order of magnitude as the
uncertainty. Examples: 3.1415±0.0001; 0.8±0.2
7) The uncertainty should be rounded to one or two significant digits.

Rules for Computation: There is always a pronounced and persistent tendency on the part of
beginners to retain too many figures in a computation. This not only involves too much work but,
worse still, leads to a fictitiously precise result.

The following rules are recommended and will save much time that would otherwise be spent in
calculation. Furthermore, their careful use will result in properly indicated accuracies.

1) In recording the result of a measurement or calculation, one, and only one, doubtful digit is
retained. For instance, a caliper whose finest division is 100-thousandths can produce a
measurement that is accurate to five decimal places at best. i.e. 3.02364.

2) In addition or subtraction, do not carry the result beyond the first column that contains a
doubtful figure. Add all figures and then round (see #4 below) the result. For example:

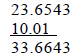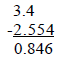which becomes 33.66	which becomes 0.8

3) In multiplication and division, carry the result to the same number of significant figures that
there are in that term which has the least number of significant figures. For example:
3.95 x 5.1 = 20.145, rounded to 2 significant figures = 20.
34.2/6.29934 = 5.429140196... becomes upon rounding 5.43

4) When “doing” mathematical manipulations with numbers that have varying numbers of
significant digits, the final result cannot have more significant digits than the least well known
digit. In practice, we will keep all the numbers to their known accuracy through out the
calculation and then round to the number of significant figures at the end. Examples:
2.0*3.14159 = 6.3; 25.001+32.0 = 55.0

5) In dropping figures that are not significant (rounding), the last figure retained should be
unchanged if the following figures dropped are less than half the previous digit. It should be
increased by 1 if the following figures dropped are greater than half the previous digit. If the last
digit dropped is 5, the preceding digit should be left unchanged if it is an even number but
increased by 1 if it is an odd number. For example:
24.5627 rounded to four significant figures becomes 24.56
34.2523 rounded to three significant figures becomes 34.3
3.485 rounded to three significant figures becomes 3.48
7.550 rounded to two significant figures becomes 7.6