Math Test #1 Solutions
 Solve the following equations:
Solve the following equations:
(a) (3 + 2x)(1 - 3x) = (6x - 1)(1 - x),
(b) x(10x - 11) = 6
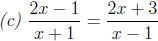
Solutions: (a) Expand both sides of the equation to
obtain:
(3+2x)(1-3x) = (6x-1)(1-x) 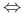 3-9x+2x-6x2 = 6x-6x2-1+x
3-9x+2x-6x2 = 6x-6x2-1+x
or
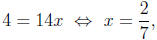
and so the solution written in set notation is
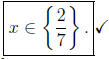
(b) Using the distributive property again we have
x(10x - 11) = 6  10x2 - 11x = 6
10x2 - 11x = 6
 10x2 - 11x - 6 = 0:
10x2 - 11x - 6 = 0:
Since the factorization method is not easy to apply here and also
the method of completing the square is still not very easy we apply
the quadratic formula a = 10, b = -11, c = -6:
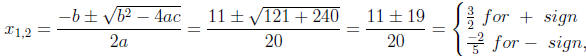
or 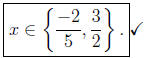 Observe that
Observe that
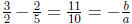 and
and 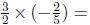
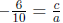 which means the
which means the
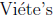 relations are satisfied.
relations are satisfied.
(c) Eliminating the denominators we have
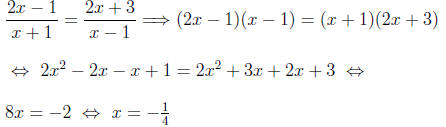
then after checking we see the only solution is
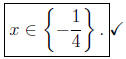
 Find all real solutions of the radical equations:
Find all real solutions of the radical equations:
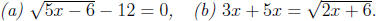
Solutions: (a) Squaring both sides, after isolating the
radical ex-
pression, we get just an implication but good enough to see how the
solutions might look like:
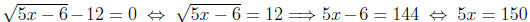
or x = 30 and after checking we see that
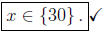
(b) Using the same method we get
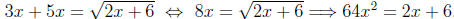
32x2 - x - 3 = 0.
Using the quadratic formula
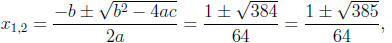
of which gives only one solution
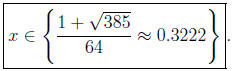
 (a) A motorboat maintained a constant speed of 18 miles
per hour
(a) A motorboat maintained a constant speed of 18 miles
per hour
relative to the water in going 8 miles upstream and then returning.
The total time for the trip was 1 hours. Use this information to find
the speed of the current.
(b) If instead of knowing that it took 1 hours for the round trip
we know that it took 20 minutes more to go upstream than to go
downstream what would be the speed of the current in this case?
Solutions: (a) If we denote by x the speed of current in miles per
hour we get that the time going upstream is 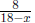 (hours) and the
(hours) and the
time going downstream is 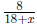 (hours). Hence
because it takes 1
(hours). Hence
because it takes 1
hour round trip we obtain the equation:
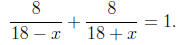
Solving this for x by adding to the same common
denominator we
get:
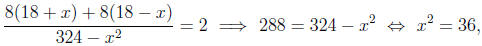
which gives 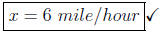 .
.
(b) Since 20 minutes is 1/3 of an hour. In this case the equation
becomes
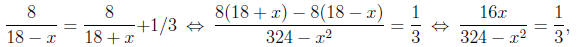
which implies
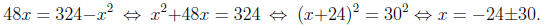
This gives only the solution 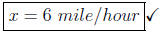 .
.
 Solve the following inequalities and write your answers in in-
Solve the following inequalities and write your answers in in-
terval notation:
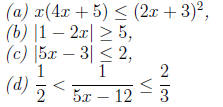
Solutions: (a) The inequality is equivalent to
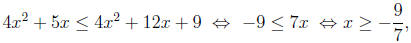
which means 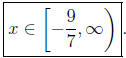
(b) The inequality becomes
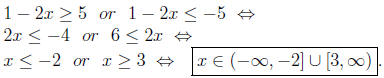
(c) In this case we have similarly
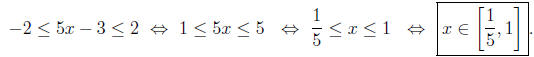
(d) Since we are dealing with positive numbers the
inequality is
equivalent to
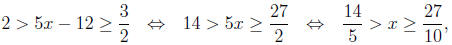
which gives 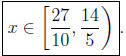
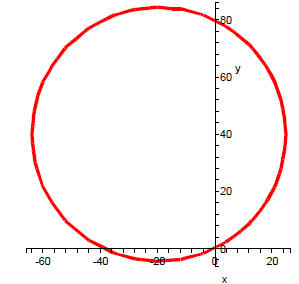
 (a) Find the center and the radius of the circle of
equation
(a) Find the center and the radius of the circle of
equation
x2 + y2 + 39x - 80y = 0.
(b) What are the coordinates of the x-intercepts ?
Solutions: (a) The equation can be written after completing the
squares
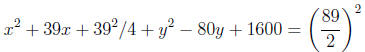
or
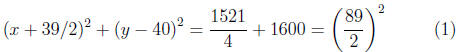
which gives the center 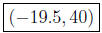 and radius
and radius 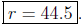
(b) Making y = 0 in x2+y2+39x-80y = 0 we obtain x2+39x = 0
which leads to two points of intersection: 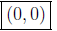 and
and 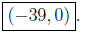
Similarly for the y-intercept we get: 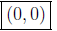 and
and
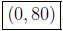 . The graph
. The graph
of this circle is included below:
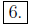 Find the equation of the line in slope intercept form
containing
Find the equation of the line in slope intercept form
containing
the point of coordinates (3,-2) and parallel to the line of equation
7x + 5y - 3 = 0.
Solutions: The slope of the given line is m =
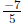 . Hence the
. Hence the
equation of the line we are looking for is y - (-2) = (-7/5)(x - 3)
or 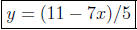 .
.
 Find the domain of the following functions
Find the domain of the following functions
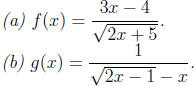
Solutions: (a) We need to impose the condition:
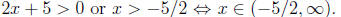
Hence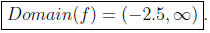
(b) In this case we have:
1. 2x - 1 ≥ 0 or 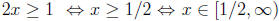 and
and
2. 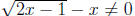 or
or 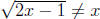 . If x
≥ 0, this is equivalent
. If x
≥ 0, this is equivalent
to 2x - 1 = x2 or 0 = x2 - 2x + 1 (completing the square)
![]()
(x - 1)2 = 0. We have only one non-negative solution: x = 1.
Therefore 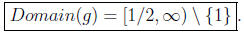
THE END


