Complex Numbers
A nonempty bounded subset of ZZ contains a maximal
element
This assertion is used several times in these notes, here is its proof.
Let m be an arbitrary element of the set M in question, there is at least one,
by assumption.
Further, let c be the bound. Then the algorithm
for n=c:-1:m do: if n ∈ M, break, fi, od
is guaranteed to halt after finitely many steps, and the current value of n is the
maximal element
of M.
Also, note the corollary that a bounded function into the integers takes on its
maximal value:
its range then contains a maximal element and any preimage of that maximal
element will do.
Complex numbers
A complex number is of the form
z = a + ib.
with a and b real numbers, called, respectively, the real part of z and
the imaginary part of z,
and i the imaginary unit, i.e.,
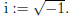
Actually, there are two complex numbers whose square is −1. We denote the other
one by −i. Be
aware that, in parts of Engineering, the symbol j is used instead of i.
MATLAB works internally with (double precision) complex numbers. Both variables
i
and j in MATLAB are initialized to the value i.
One adds complex numbers by adding separately their real and imaginary parts.
One multiplies
two complex numbers by multiplying out and rearranging, mindful of the fact that
i2 = −1. Thus,
(a + ib)(c + id) = ac + aid + bic − bd = (ac − bd) + i(ad + bc).
Note that both addition and multiplication of complex numbers is commutative.
Further, the
product of z = a + ib with its complex conjugate
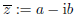
is the nonnegative number
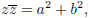
and its (nonnegative) squareroot is called the absolute value or modulus of z
and denoted by
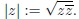
For z ≠ 0, we have l z l ≠ 0, hence
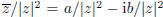 is a well-defined complex number. It
is a well-defined complex number. It
is the reciprocal of z since
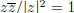 ,
of use for division by z. Note that, for any two complex
,
of use for division by z. Note that, for any two complex
numbers z and
 ,
,
It is very useful to visualize complex numbers as points in the so called
complex plane, i.e.,
to identify the complex number a + ib with the point (a, b) in IR2. With this identification, its
absolute value corresponds to the (Euclidean) distance of the corresponding
point from the origin.
The sum of two complex numbers corresponds to the vector
sum of their corresponding points. The
product of two complex numbers is most easily visualized in terms of the polar
form
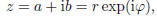
with r ≥ 0, hence r = l z l its modulus, and 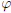 ∈ IR is called its
argument. Indeed,
for any real
∈ IR is called its
argument. Indeed,
for any real  ,
,
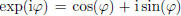 has absolute value 1, and
has absolute value 1, and
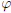 is the angle (in
radians) that the vector
is the angle (in
radians) that the vector
(a, b) makes with the positive real axis. Note that, for z ≠ 0, the argument,
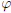 ,
is only defined up to
,
is only defined up to
a multiple of 2π , while, for z = 0, the argument is arbitrary. If now also
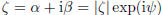 ,
,
then, by the law of exponents,
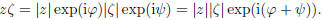
Thus, as already noted, the absolute value of the product is the product of the
absolute values of
the factors, while the argument of a product is the sum of the arguments of the
factors.
For example, in as much as the argument of 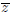 is the negative of the argument of
z, the argument
is the negative of the argument of
z, the argument
of the product 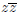 is necessarily 0. As another example, if z = a + ib is of
modulus 1, then z lies
is necessarily 0. As another example, if z = a + ib is of
modulus 1, then z lies
on the unit circle in the complex plane, and so does any power zk of
z. In fact, then 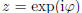
for some real number 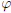 , and therefore
, and therefore
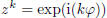 . Hence, the sequence
. Hence, the sequence
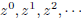 , appears
, appears
as a sequence of points on the unit circle, equally spaced around that circle,
never accumulating
anywhere unless  = 0, i.e., unless z = 1.
= 0, i.e., unless z = 1.
(17.1) Lemma: Let z be a complex number of
modulus 1. Then the sequence 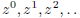 of powers of z lies on the unit circle, but fails to converge except when z = 1. |
Convergence of a scalar sequence
A subset Z of C is said to be bounded if it lies in some ball
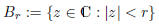
of ( finite) radius r. Equivalently, Z is bounded if, for some r,
![]() < r for all
< r for all
![]() ∈ Z. In either case,
∈ Z. In either case,
the number r is called a bound for Z.
In particular, we say that the scalar sequence 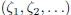 is
bounded if the set
is
bounded if the set 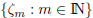
is bounded. For example, the sequence (1, 2, 3, ...) is not bounded.
(17.2) Lemma: The sequence
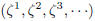 is
bounded if and only if is
bounded if and only if 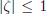 . Here, . Here,
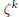 denotes the kth power of the scalar z. |
Poof: Assume that
![]() > 1. I claim that, for all m,
> 1. I claim that, for all m,
(17.3)
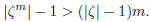
This is certainly true for m = 1. Assume it correct for m = k. Then
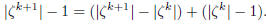
The first term on the right-hand side gives
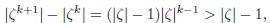
since ![]() > 1, while, for
the second term,
> 1, while, for
the second term, 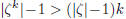 by induction
hypothesis. Consequently,
by induction
hypothesis. Consequently,
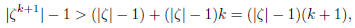
showing that (17.3) also holds for m = k + 1.
In particular, for any given c, choosing m to be any natural number bigger than
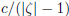 ,
,
we have 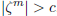 . We conclude that the sequence
. We conclude that the sequence
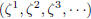 is unbounded when
is unbounded when
![]() > 1.
> 1.
Assume that 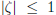 . Then, for any m,
. Then, for any m,
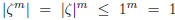 , hence the sequence
, hence the sequence
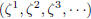 is not only bounded, it lies entirely in the
unit disk
is not only bounded, it lies entirely in the
unit disk
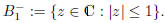
A sequence 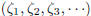 of (real or complex) scalars is said to
converge to the
scalar
of (real or complex) scalars is said to
converge to the
scalar ![]() , in
, in
symbols:
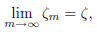
if, for all ε > 0, there is some 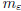 so
that, for all
so
that, for all 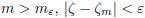 .
.
Assuming without loss the scalars to be complex, we can profitably visualize this
definition as
saying the following: Whatever small circle 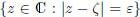 of radius ε we
draw around the
of radius ε we
draw around the
point ![]() , all the terms of the sequence except the
first few are inside that circle.
, all the terms of the sequence except the
first few are inside that circle.
| (17.4) Lemma: A convergent sequence is bounded. |
Proof: If 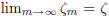 , then
there is some
, then
there is some 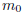 so that, for all
so that, for all
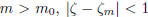 .
.
Therefore, for all m,
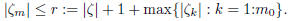
Note that r is indeed a well-defined nonnegative number, since a finite set of real
numbers always
has a largest element.
| (17.5) Lemma: The sequence
else 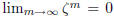 , while in the latter case , while in the latter case
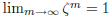 . . |
Proof: Since the sequence is not even bounded when
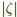 > 1, it cannot be convergent in
> 1, it cannot be convergent in
that case. We already noted that it cannot be convergent when
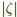 = 1 unless
= 1 unless
![]() =
1, and in that
=
1, and in that
case 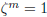 for all m, hence also
for all m, hence also
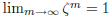 .
.
This leaves the case 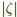 < 1. Then either
< 1. Then either
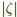 = 0, in which case
= 0, in which case
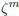 = 0 for all
m, hence also
= 0 for all
m, hence also
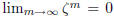 . Else, 0 <
. Else, 0 <
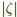 < 1, therefore
< 1, therefore
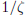 is a well-defined complex number of
modulus
is a well-defined complex number of
modulus
greater than one, hence, as we showed earlier,
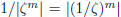 grows
monotonely to infinity as
grows
monotonely to infinity as
m→∞. But this says that 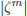 decreases monotonely to 0. In other words,
decreases monotonely to 0. In other words,
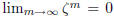 .
.
Horner, or: How to divide a polynomial by a linear factor
Recall that, given the polynomial p and one of its roots, μ, the polynomial
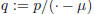 can
can
be constructed by synthetic division. This process is also known as nested
multiplication or
Horner's scheme as it is used, more generally, to evaluate a polynomial efficiently. Here are the
details, for a polynomial of degree ≤ 3.
If 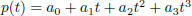 , and z is any scalar, then
, and z is any scalar, then
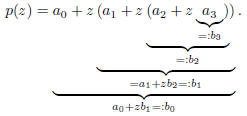
In other words, we write such a polynomial in nested form
and then evaluate from the inside out.
Each step is of the form
"horner (17.6) 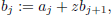
it involves one multiplication and one addition. The last number calculated is
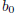 , it is the value
, it is the value
of p at z. There are 3 such steps for our cubic polynomial (the definition
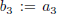 requires no
requires no
calculation!). So, for a polynomial of degree n, we would use n multiplications
and n additions.
Now, not only is 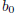 of interest, since it equals p(z), the other
of interest, since it equals p(z), the other
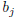 are also
useful since
are also
useful since
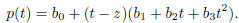
We verify this by multiplying out and rearranging terms according to powers of
t. This gives
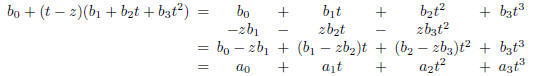
The last equality holds since, by (17.6),
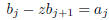
for j < 3 while 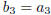 by definition.
by definition.
(17.7) Nested Multiplication (aka Horner): To
evaluate the polynomial 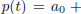 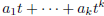 at the point z, compute the sequence at the point z, compute the sequence
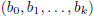 by the prescription
by the prescription
Then q(t) = p(t)/(t − z). |
Since p(t) = (t − z)q(t), it follows that degq < deg p.
This provides another proof (see (3.21))
for the easy part of the Fundamental Theorem of Algebra, namely that a
polynomial of degree k
has at most k roots.



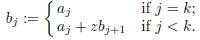
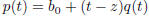 , with
, with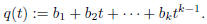
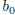 = 0), then
= 0), then