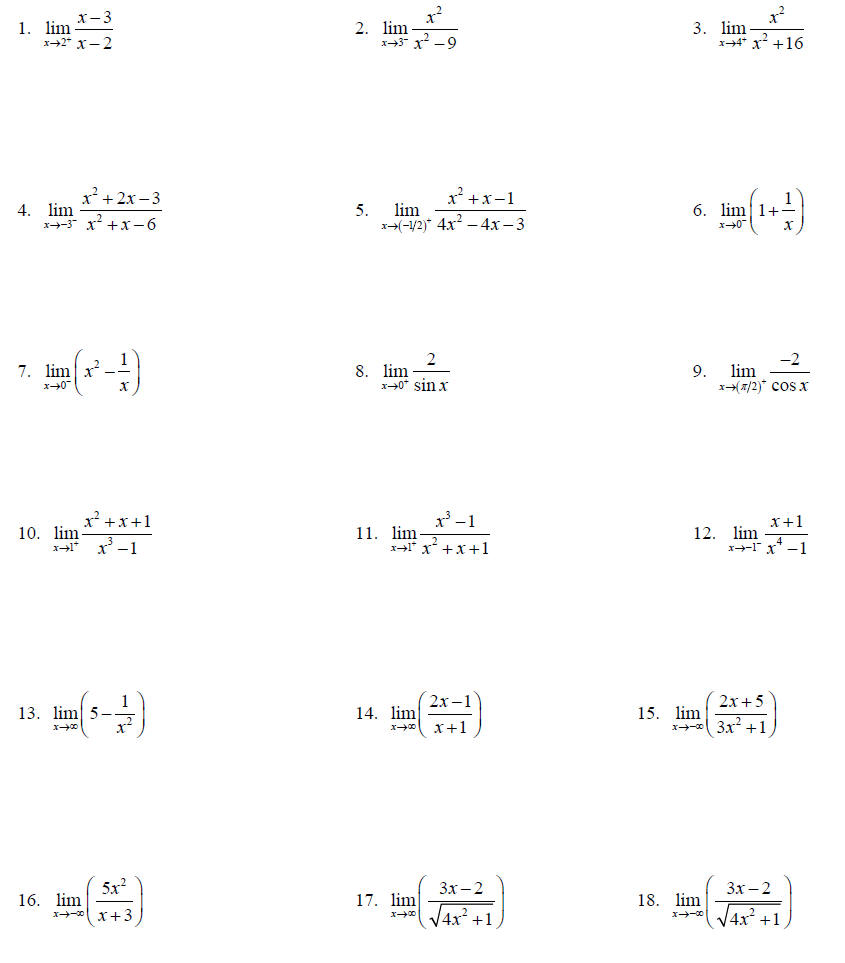Fractional and Negative Exponents
Simplify using only positive exponents.
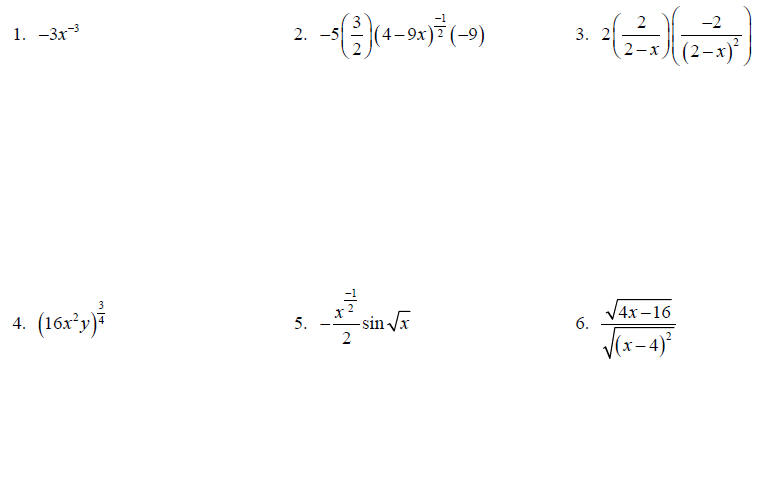
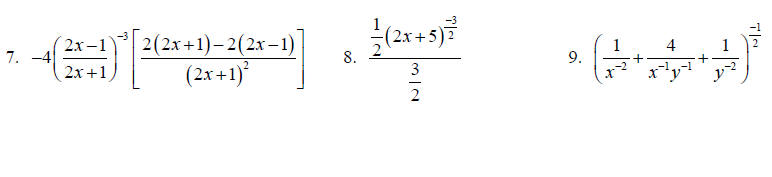
Topic 2: Domain and Discontinuity
Find the domain of the following functions and describe the discontinuity, if any, as removable or non-removable.

Topic 3: Solving Inequalities
Write the following absolute value equations as piecewise equations.
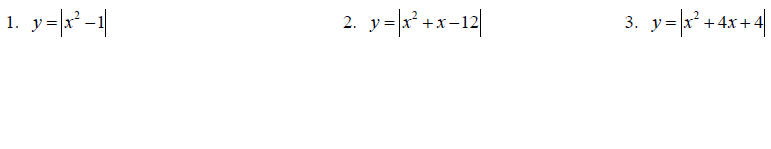
Solve the following by factoring and making appropriate sign charts.
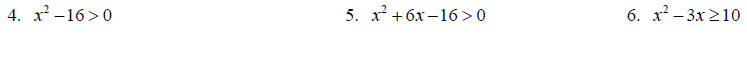
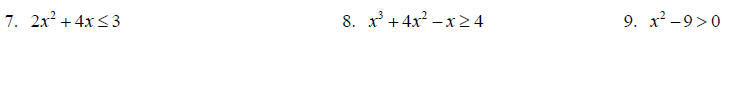
Topic 4: Special Factorization
Factor completely.
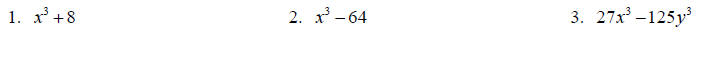
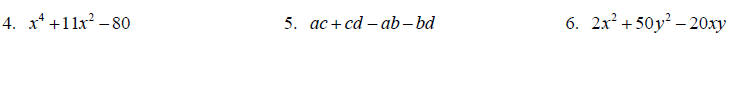
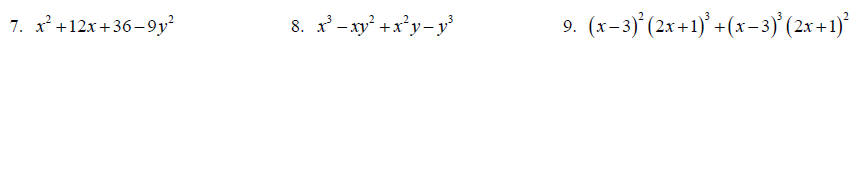
Topic 5: Function Transformation
If f (x) = x^2 −1, describe in words, using correct
mathematical terminology, what the following would do to the
graph of f ( x).
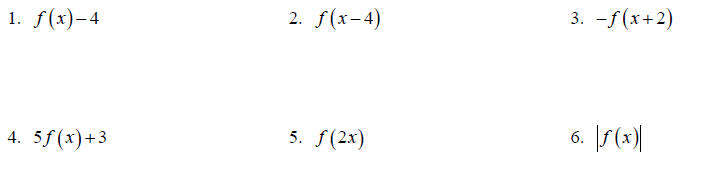
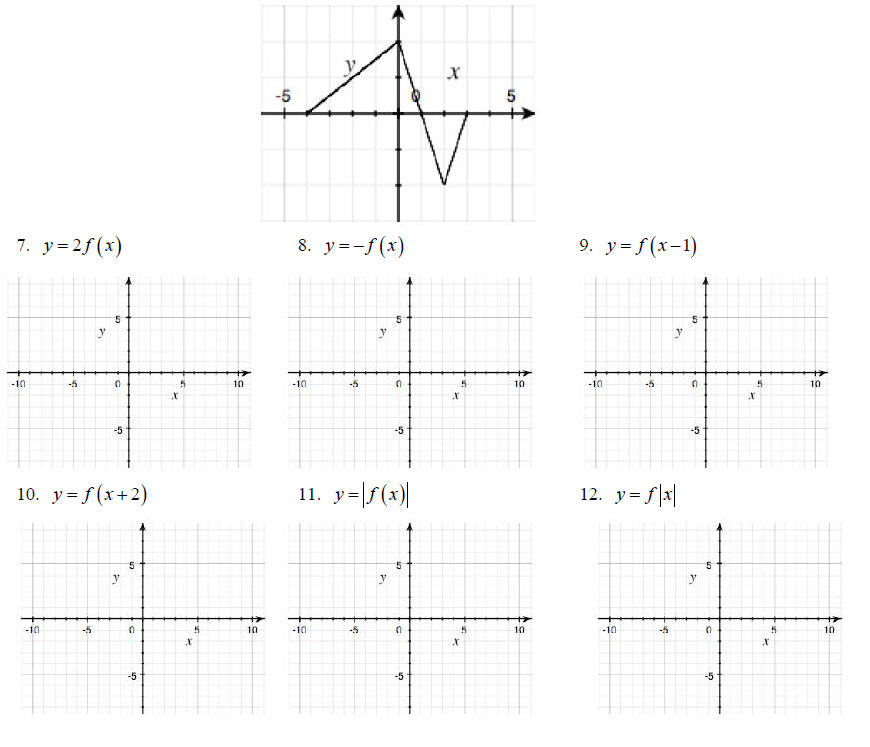
Using the following graph of y = f (x), sketch the following graphs.
Topic 6: Even and Odd Functions
Determine if the relation is even, odd or neither analytically.
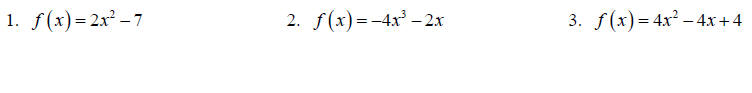
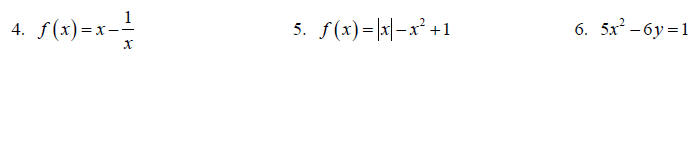
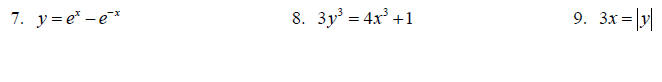
Topic 7: Solving Quadratic Equations
Solve each equation.
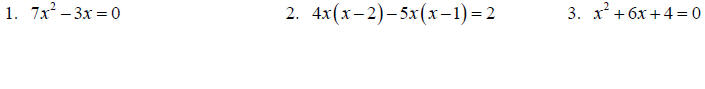
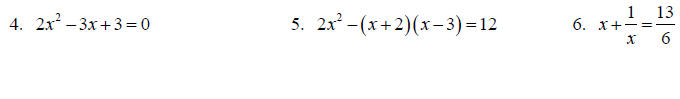
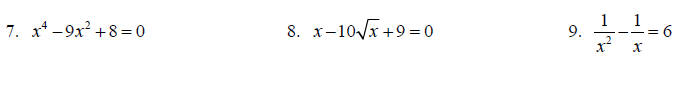
Topic 8: Asymptotes
Find the equations for all asymptotes, if any exist, for each function.
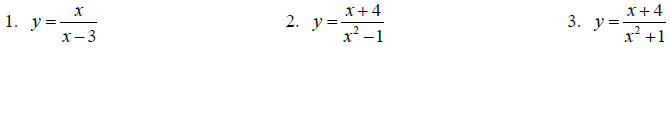
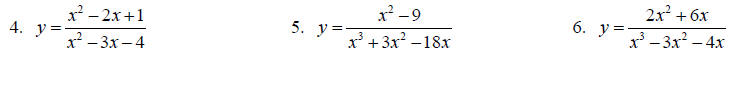
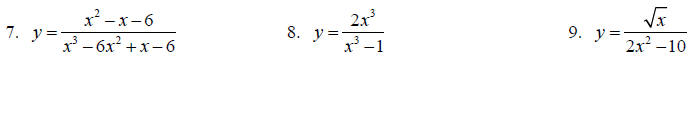
Topic 9: Complex Fractions
Simplify the following.
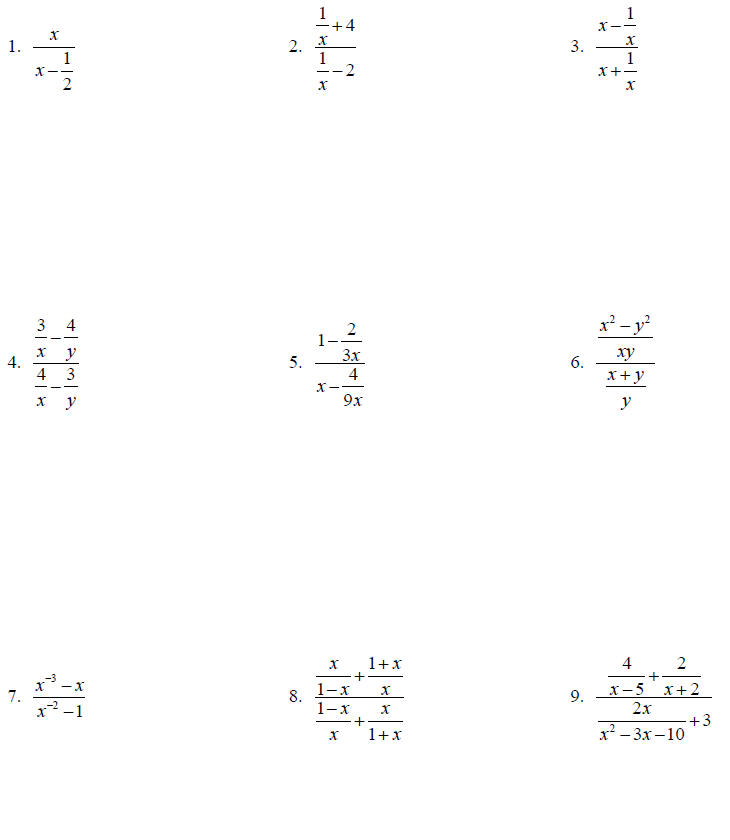
Topic 10: Composition of Functions
If 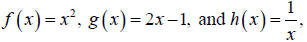 find the following.
For 6-9 state the domain of the resulting
find the following.
For 6-9 state the domain of the resulting
function.
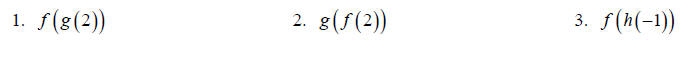
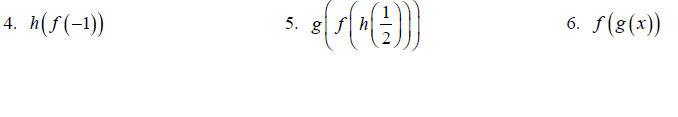
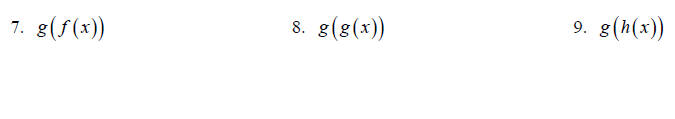
Topic 11: Solving Rational equations
Solve each equation for x.
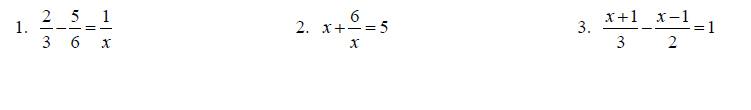
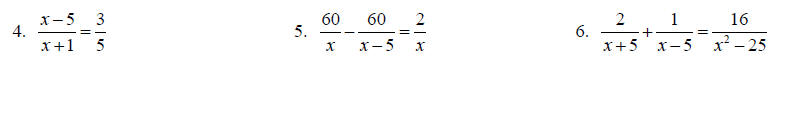
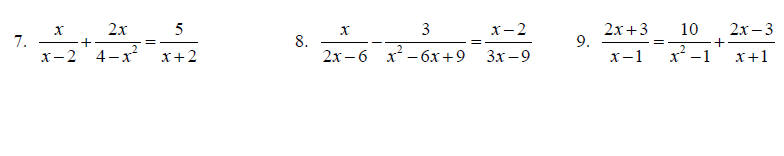
Topic 12: Logarithmic Function
Write each expression as a sum and/or difference without exponents.
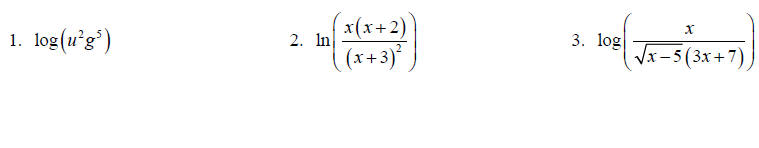
Write each expression as a single logarithm.
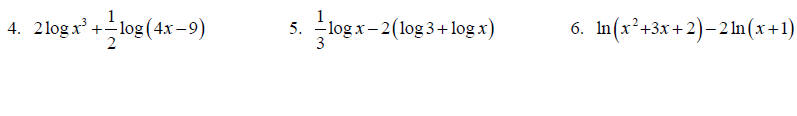
Solve each equation for x.
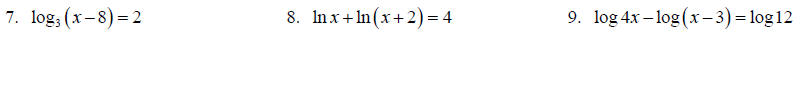
Topic 13: Exponential Function
Solve each of the following for x.
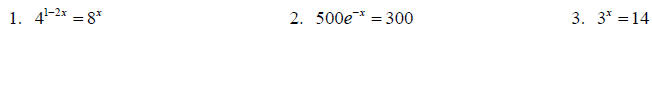
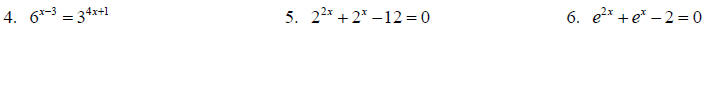
Solve each of the following.
7. Which rate would yield more after 1 year starting with $500?
5 ½ % compounded quarterly 6 ¼ % compounded monthly 9% compounded annually
8. If a population increased from 300,000 to 450,000 from 2001 to 2004, what will the population be in 2007?
9. The half-life of carbon 14 is 5600 years. A piece of
charcoal is found to contain 70% of the carbon 14 that it
originally had. When did the tree from which the charcoal came die?
Topic 14: Trig Identities
Establish each trig identity.
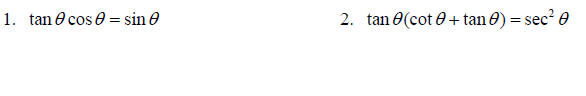
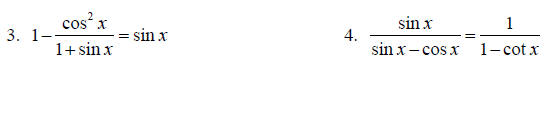
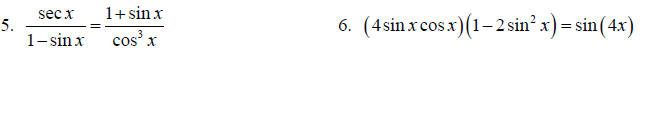
Topic 15: Trig equations
Solve each equation for x on the interval [0,2π ].
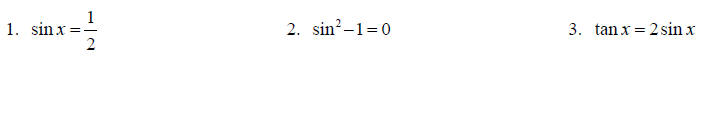
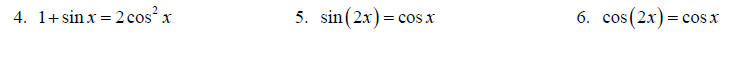
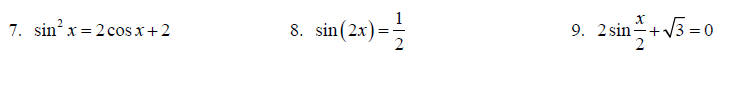
Topic 16: Limits Algebraically
Find each limit analytically
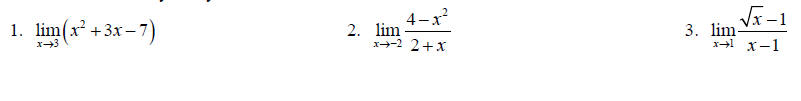
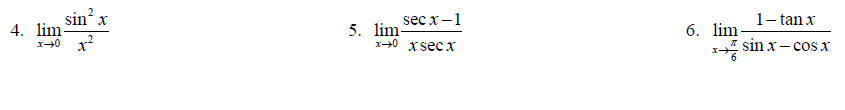

9. If 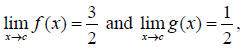 find
find

10. If 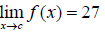 find
find

Topic 17: Limits at Infinity
Solve each limit without a calculator.