Matrices and Determinants
A matrix looks like:
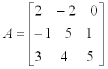
You read this as a “three by three matrix” (3 X 3 Matrix).
This means that there are 3
rows (horizontals) and 3 columns (vertical). Each number in a matrix is called
an
“element” and is referred to by the row number and then the column number. For
example, -2 is in row 1, column 2 or in the a12 position.
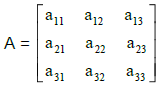Here the capital letter
“A” names the entire matrix (Matrix A).
The lowercase letter “a” represents the position of each element using the
subscripts in
the format of row, then column.
Create the following 2 x 2 matrix below: Place 3 in a11 , 4 in
a12
, 6 in a21 , and 7 in a22 .
When you are adding and subtracting matrices, the order of
each matrix must be same. This
means that each matrix must have the same number of rows and columns.
Below, two matrices are being added. Notice each matrix is of the order 2 X 3.
Addition or
subtraction of matrices that do not have the same order is impossible.
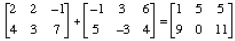
To add matrices, simply add the values of each
corresponding element: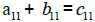 
and so forth.