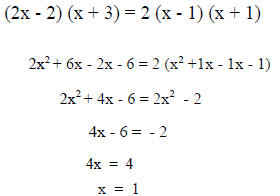Math 111 Chapter 1 Sections 1 & 2 Reviews
MTH ·111·First ·day · Review
 Name Name
   Solve · and · check Solve · and · check
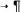  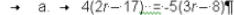  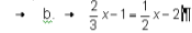   A · student · multiplies · each ·
side · of · the · equation · A · student · multiplies · each ·
side · of · the · equation · 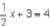 · · by · 2 ·
and · produces · the · · by · 2 ·
and · produces · theequation 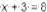 · · Has · the · student ·
produced · an · equivalent · equation ? · · Explain . · · Has · the · student ·
produced · an · equivalent · equation ? · · Explain .  |
| 3. Suppose we attempt to solve the equation 4x =
7x by first dividing each side of the equation by x. The result is 4 = 7, which is not true. Explain what happened.
|
| Mth 111 Topics Chapter 1 Overview Section 1.1 Solving Linear Equations  Solving Linear Equations involving
distributive property Solving Linear Equations involving
distributive propertyand foil  Solving literal equations Solving literal equations Applications average, Applications average,mixture, uniform motion, work Section 1.2  Solving quadratics: Solving quadratics:o by factoring and zero product principle; o square root; o completing the square; o quadratic formula;  Discriminant Discriminant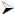 Applications: square box, tossing an object Applications: square box, tossing an object |
| Forming Equivalent Equations An equation can be rewritten into an equivalent form by: 1. Simplify either side 2. Using the Golden Rule of Algebra Do unto one side as thou hath done unto the other 3x = 7y equivalent to 3x + 5 = 7y + 5 3. Interchanging sides |
| Linear Equations : A linear equation in a single variable x is an equation that can be written in the form ax + b = 0 where a and b are real numbers, with a not 0. Solve 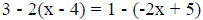 |
| Solve
|
| Literals Equations : formulas with several
unknowns 1. 10 = a - 4x, solve for x 2. 8 = ax + 3x , solve for x 3. P = S - dt,
solve for t |
| Word Problems 1. What do you need to know to solve the problem? Write this down in English. 2. Assign numbers to the known parts. Assign a letter to the unknown parts 3. Translate this into an algebraic equation or inequality. 4. Solve. 5. Make sure that your solution answers the original question |
| Useful Formulas Business: Revenue = Profit - Cost Simple Interest : I = Prt Mixtures: (1st % × Amt) + (2nd % × Amt) = Final % × Amt Rate problems: Distance = rate × time Work Problems: (part done by A ) + (part done by B) = 1 whole job Averages: 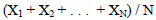 |
| Applications: Averages: 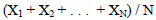 The average on your four tests is 91.25. Your test scores are 92, 86, and 98 with one test score gone missing. Find it! |
| Simple Interest : I = Prt You invest part of a $10,000 bonus in a 2% simple interest account and the remainder of the money at 5% simple interest. Together the investments earn $400 per year. find the amount at each rate. let x be amount in 2% let 10000 - x be amount in 5% t = 1 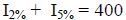 |
| Rate problems : Distance = rate × time
Example : Two boats traveling the same direction
leave a harbor at First we need to picture the situation. Let A be the slower boat and B be the faster one. Let x mph be the average rate of boat A. The
average rate of boat B is 2x
(average rate of B)(time) – (average rate of A)(time)
= 60 |
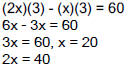 The average rates are 20 mph and 40 mph |



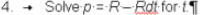
 A · student · solves · the · literal ·
equation ·
A · student · solves · the · literal ·
equation ·  · for · the · variable ·
P. ·The · student's
· for · the · variable ·
P. ·The · student's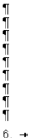 A · tutor · states · that · the ·
formula ·
A · tutor · states · that · the ·
formula · 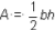 · can · also · be ·
expressed · as
· can · also · be ·
expressed · as 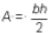 .· · Do ·
.· · Do ·