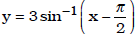OBJECTIVES FOR THE MMPT
K. Piecewise-Defined Functions
Be able to:
• graph a given piecewise defined function.
Ex. Graph: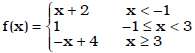 
, also, what is f(2)?
• match the graph of a piecewise-defined function with its equation.
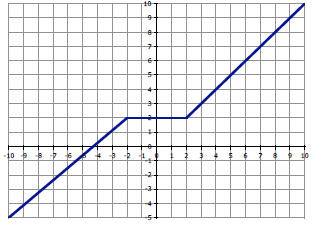
Ex. Determine the equations of the piecewise-defined function whose graph is
given below, along with their respective domain
L. Polynomial Functions
Be able to:
• determine the end-behavior of a given polynomial function
Ex. What is the end behavior of the function y = 2x5 − 4x3 + 5x − 3 ?
• find the y-intercept and the x-intercepts of polynomial
functions that factor easily over
the integers
Ex. Find the y- & x-intercepts of the polynomial function: y = x4 −13x2 + 36 ;
• find the multiplicity of the real zeros of a polynomial function
Ex. find all the zeros of the function y = x4 −13x2 + 36 and state their
multiplicities.
• match the graph of polynomial functions with their equations
Ex. Which of the graphs below best represents the function
y = (x + 3)(x +1)2(x − 2) ?
M. Rational Functions
Be able to:
• do a long division of a polynomial by a polynomial
Ex. Divide: x4 − 3x3 + 5x2 +1 by x2 + 2 using long division.
• determine the horizontal and vertical asymptotes of rational functions
Ex. Determine the vertical and horizontal asymptotes of
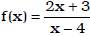
• determine the y- & x- intercepts of rational functions, if any
Ex. Determine the x- & y intercepts of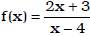
• match the graph of rational functions with their equation.
Ex. Which of the following equations best matches the given graph?
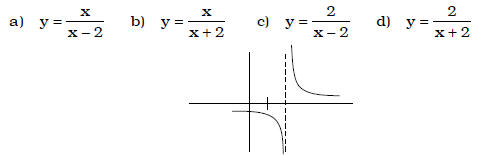
N. Exponential Functions
Be able to:
• match the graph of of exponential functions of the form: f (x) = C · ba(x-h) +
k with its
equation.
Ex. The function f(x) has the same graph as the one of y = 2x but shrunk
vertically by a scaling factor of 1/2, then reflected about the x-axis, and then
shifted down 4 units. What is the equation of f(x)?
• determine the equation of the horizontal asymptote of
such functions
Ex. What is the horizontal asymptote of the function g(x) = −3e-x − 5 ?
• determine the y- & x-intercept(s) of such functions
Ex. What are the x- and y- intercepts of the function: f (x) = 2x − 8 ?
• match the graphs of such functions with their equations.
Ex. The sketch below is that of which function?
O. Logarithmic Functions & Properties of Logarithms
Be able to:
• express a logarithmic form into exponential form and an exponential form into
logarithmic
form.
Ex. Express in exponential form: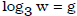 
Ex. Express in logarithmic form: 34 = 81.
• match the graphs of logarithmic functions of the form:
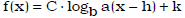with their
equation.
Ex. Which graph could be the one of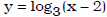 
?
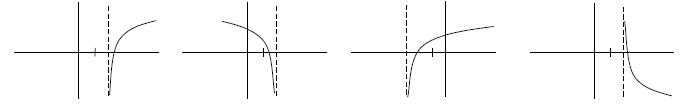
• determine the equation of the vertical asymptote of such
functions
Ex. What is the vertical asymptote of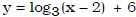 
?
• determine the x- & y-intercepts of such functions
Ex. Determine the x & y intercept of the function:
;
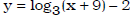• apply the properties of logarithms to evaluate or simplify logarithmic
expressions
Ex. Express as a single log and simplify:
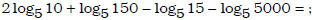
P. Translate from Degrees into Radians (or π-radians) and from Radians into
Degrees
Ex. 135° is how may π radians?
Q. Trig Ratios of the Special Angles (0°, 30°,60°, 90°)
Be able to:
• determine the trig ratio of angles that can be deduced from those of the
special angles
(0°, 30°,60°, 90°).
Ex. find the exact value of cos135°;
• determine the inverse trig value of certain numbers such as: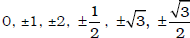 
,
etc.
Ex. Find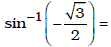 
;
R. Trig Ratios of Angles
Be able to:
• determine all the other five trig ratios of an angle, given the value of one
of its trig ratios
and the quadrant in which the terminal side of the angle lies.
Ex. If sec(x) = – 2 and the terminal side of x is in QII, What is sin(x)?
• Given one of the trig ratios of an angle x determine the trig ratios of the
angles: –x, (π –
x) or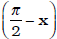 
.
Ex. Given sinx = -1/2, and that the terminal side of x is in QIII, find tan (π/2
– x);
• Use the sum, difference, half-angle and double-angle formulas to determine the
trig
ratios of other angles.
Ex. Without a calculator, evaluate sin(π/6).
S. Solve triangles
Be able to:
• solve a right triangle given some of the sides or angles.
Ex. The longer leg of a right triangle is 10 units. The angle opposite to the
longer
leg is 30°. Solve the triangle.
• apply the law of sines and the law of cosines to solve oblique triangles.
Ex. in an oblique triangle ABC, the measure of angle A is 60°. If AB = 10 cm &
AC = 14 cm, What is the length of the side BC?
T. Graphing Trig Functions & their Inverses
Be able to:
• Match trig functions or inverse trig functions of the form given below with
their graph.
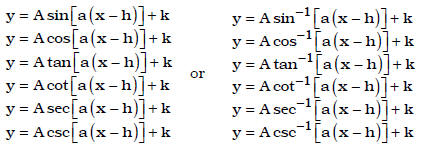
Ex. Describe the graph of
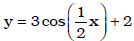as compared to the graph of
y = cos(x) using rigid &/or non-rigid transformations. In
the same coordinate
plane sketch the graph of y = cos(x) and that of
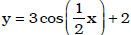
Ex. Describe the graph of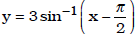 
as compared to the graph of
y = sin-1(x) using rigid &/or non-rigid transformations. In the same coordinate
plane sketch the graph of y = sin -1(x) and that of