Finite Math Lines and Such

The problems here are a review of what you should already know about lines and linear
inequalities. This reviews the material in sections 1.1 - 1.4.

Standard Form of a Linear Equation (aka: Slope-Intercept form): y = mx + b General Equation: cx + dy = e Point-Slope Formula (to find the equation of a line): 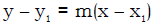Equation of a Vertical Line: x = a Equation of a Horizontal Line: y = b

Practice

1. Put these in standard form:
a. 4y – 2x = 7 + y
b. 3x – 2y = 8

2. Put the inequality in standard form:
a. 3y – 4x ≥ x + 5
b. x – 2y < 4 + 2x

3. Find the equation of the line . . . (put in standard form)
a. . . . through the points (–1, 2) and (4, 12).
b. . . . through the points (4, 5) and (2, 5).
c. . . . parallel to the line 2y – 4x = 6 and through the point (1, 3).
d. . . . perpendicular to the line 2y – 4x = 6 and through the point (1, 3).

4.
a. Find the equation of the vertical line through the point (-3, 4).
b. Find the equation of the horizontal line through the point (-3, 4).

5. Find the point of intersection of the lines y = 2x – 3 and 2y + 4x = 8.

6. Graph the following (label important points):
a. 3x – 2y = 6
b. 4x + y = 2 and y = 2x + 5
c. line going through (1, 3), with slope –2.
d. y < 2x + 3
e. y ≥ x – 4 and 3x + y < 8

Application

1. There is a linear relationship between Celsius temperature readings and
Fahrenheit temperature readings. The relationship is as follows:

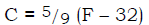
a. Put this in slope-intercept form.
b. Find the Celsius reading for 80° Fahrenheit.
c. At what Fahrenheit temperature is Celsius 90°?
d. If the Fahrenheit changes by 1°, by how much does the Celsius change?

2. In economics, we spend a lot of time studying supply and demand curves
and the factors that affect them. These curves are in terms of price (p) and
quantity (q). The equilibrium point is where the two curves intersect.
Suppose that the Widget Manufacturing Company has a supply curve given
by q = 2500 p – 4000 and a demand curve given by 1000 p + q = 12,000.
Find the equilibrium point and interpret the values.

3. At a price of $100, the Gadget Manufacturing Company can supply 1000 of
their product. For $175, they will supply 2500.
a. Find the equation for the supply curve.
b. If the price is $0, what will supply be? What does this mean?

4. An apartment complex has a storage tank to hold its heating oil. The tank
was filled on January 1, but no more deliveries of oil will be made until
sometime in March. Let t denote the number of days after January 1 and
let y denote the number of gallons of fuel oil in the tank. Current records
show that y and t will be related by the equation y = 30,000 – 400 t.
a. Graph the equation.
b. How much oil will be in the tank on February 1?
c. How much oil will be in the tank on February 15?
d. Determine the y-intercept of the graph. Explain its significance.
e. Explain the significance of the slope.
f. Determine the t-intercept of the graph. Explain its significance.