Additional Topics With Rational Numbers
In this section we will consider some additional topics,
and revisit some old topics, involving
rational numbers. Our first topic involves ordering and comparing the size of
rational numbers.
Which fraction is larger: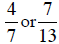
? Recall in Section
3.1 we answered this question by converting
to decimal form. An alternate approach is to build each fraction to a common
denominator,
which is 7 •13 = 91. Converting each fraction:
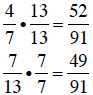
Since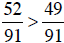 
, then
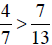. This approach is usually faster than
converting to decimal,
especially as the denominators of the fractions become larger.
Example 1 Replace the blank with the correct symbol: <, =, or >
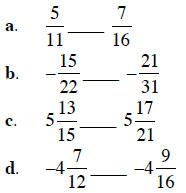
Solution a. Building each fraction to a common denominator:
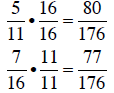
Since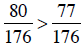 
, then
.
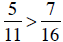b. Building each fraction to a common denominator:
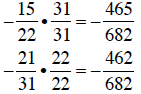
Since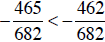 
, then
.
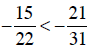c. Building each fraction to a common denominator:
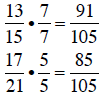
Since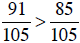 
, then
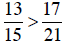and so 
.
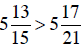d. Building each fraction to a common denominator:
Since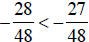 
, then
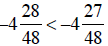and so 
.
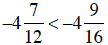Not only can we determine the order of rational numbers,
we can represent this order by means
of graphing inequalities. Recall that the number line is ordered by the <
symbol; that is, as
numbers which are smaller appear to the left of numbers which are larger.
Suppose we were
presented with the inequality x < 4 . We can use a number line to “shade” those
numbers which
are less than 4 (remember, that means “to the left of” 4). Note the use of the
open circle ( ○ ) at
the number 4, indicating that 4 is not part of the shaded portion.
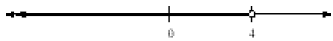
Now consider the inequality x ≥ -2 . We now must shade
those numbers greater than or equal to
–2, which means numbers “to the right of” –2. Note the use of the closed circle
(• ) at the
number –2, indicating that –2 is part of the shaded portion.
Example 2 Graph the given inequality.
a. x > !5
b. x < 2
c.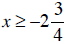 
d. x ≤ -3.6
Solution a. Starting at –5, shade all values to the right
of –5. Since the inequality is >,
we use the open circle at –5, indicating it is not included in the shading:
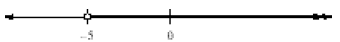
b. Starting at 2, shade all values to the left of 2. Since
the inequality is <, we
use the open circle at 2, indicating it is not included in the shading:
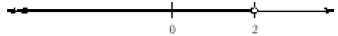
c. Starting at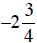 
, shade
all values to the right of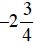 
. Since the
inequality
is ≥, use the closed circle at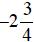 
, indicating
it is included in the shading:
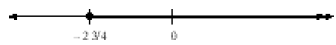
d. Starting at –3.6, shade all values to the left of –3.6.
Since the inequality is ≤,
use t he closed circle at –3.6, indicating it is included in the shading:
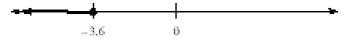
Recall in the last chapter we considered integer solutions
to equations. We now consider rational
number solutions to equations. Recall that a number is a solution to an equation
if, after replacing
the variable in the equation with the number, a true statement results. The
following example
will illustrate this process.
Example 3 Determine whether or not the given rational number is a solution to the equation.
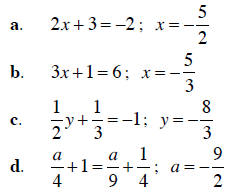
Solution a. Substitute x = -5/2 into the equation evaluate the left side:
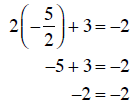
Since this last statement (–2 = –2) is true, x = -5/2 is a
solution to the
Equation 2x + 3 = -2 .
b. Substitute x = -5/3 into the equation and evaluate the left side:
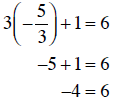
Since this last statement (–4 = 6) is false, x = -5/3 is
not a solution to the
Equation 3x + 1 = 6 .
c. Substitute y = -8/3 into the equation and evaluate the left side:
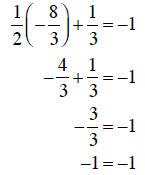
Since this last statement (–1 = –1) is true, y = -8/3 is a
solution to the
Equation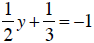 
d. Substitute a = -9/2 into the equation and evaluate both sides:
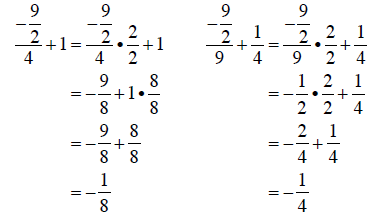
Since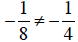 
, the two sides
do not evaluate to the same number, so
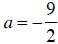is not a solution to the equation
.
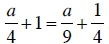Another topic studied in the last chapter was that of
arithmetic and geometric sequences.
Recall that an arithmetic sequence is one in which each term is the result of
adding a common
difference onto the previous term, while a geometric sequence is one in which
each term is the
result of multiplying a common ratio by the previous term. Now we consider
sequences in which
rational numbers are involved.