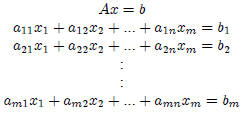Linear Algebra
Exercise 1 Solve the system using matrix method:
x1 + x2 = 1
x1 - x2 = 3
-x1 + 2x2 = -2
Exercise 2 Solve the system using matrix method
-x1 + x2 - x3 + 3x4 = 0
3x1 + x2 - x3 - x4 = 0
2x1 - x2 - x3 - x4 = 0
Exercise 3 In the downtown section of a certain city, two sets of one way
streets intersect as shown below. The average hourly volume traffic entering and
leaving this section during rush hour is given in the diagram. Determine the
amount of traffic between each of the four intersections.
Rank, Uniqueness and Consistency As the exercises suggest, there are
two fundamental questions that we may want to address when we are solving
for a system of linear equations
1) Is the system consistent? (Does a solution exist?)
2) If a solution exists, is it unique? (Is there one and only one
solution?)
We can determine whether one infinite, or no solutions exist if we know (1)
the number of equations m, (2) the number of unknowns n, and (3) the rank of
the matrix representing the linear system.
Rank: number of nonzero rows in its row echelon form.
Example 4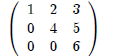
Rank = 3
Example 5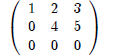
Rank = 2
Example 6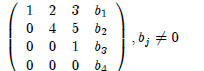
Rank = 4
Let A be the coefficient matrix and
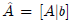be the augmented matrix.
Then,
1. rank A ≤ rank Â
Augmenting A with b can never result in more zero rows than originally
in A itself. Suppose row i in A is all zeros and that bi is non-zero. Aug-
menting A with b will yield a non-zero row i in Â.
2. rank A ≤ rows A
By definition of a rank.3
3. rank A ≤ columns A
Suppose there are more rows than columns (otherwise the previous rule
applies). Each column can contain at most one pivot. By pivoting, all
other entries in a column below the pivot are zeroed. Hence, there will
only be as many non-zero rows as pivots, which will equal the number of
columns.
Existence of solutions:
1. Exactly one solution
rank A = rank  = rows A = columns A
Necessary condition for a system to have a unique solution: that there be
exactly as many equations as unknowns.
2. Infinite solutions
rank A = rank; and columns A > rank A
If a system has a solution and has more unknowns than equations, then
it has infinitely many solutions.
3. No solution
rank A < rank Â
Then there is a zero-row i in A's reduced echelon that corresponds to a
non-zero row i in Â's reduced echelon. Row i of the translates to the
equation:
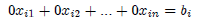
Where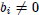 
. Hence, the system has no solution.
Exercise 7
x1 + 2x2 + x3 = 1
2x1 + 4x2 + 2x3 = 3
Exercise 8
x1 + x2 + x3 + x4 + x5 = 2
x1 + x2 + x3 + 2x4 + 2x5 = 3
x1 + x2 + x3 + 2x4 + 3x5 = 2
2 Linear Algebra: Module 2
2.1 Module Topics:
Linear Independence
Matrix Algebra
Inverse
Determinants
Cramers Rule
Eigenvalues & Eigenvectors
2.1.1 Linear Independence
Let v1, v2, …, vn be a set of n vectors each of which is of order m. Then the
set
of vectors is linearly dependent if there exist scalars a1, a2, …, an at least
one of
which is not 0 such that
a1v1 + a2v2 + a3v3 + … + anvn = 0
Or
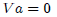
Example 9 Is there linear dependence?
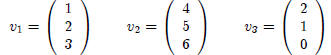
Hint: We can try to augment these vectors into a matrix and solve for a
reduced row echelon form and see if we can find some relationship between the
rows. If we can determine some functional linear relationship between these
vectors, we can say that there is linear dependence.
2.1.2 Matrix Algebra
Matrix: A matrix is an array of mn real numbers arranged in m rows by n
column.
Matrix addition (or subtraction): Let A and B be two m
× n matrices.
Then
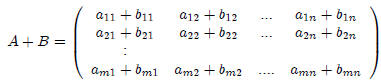
Note: A and B must be the same size!
Example 10
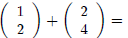
Example 11
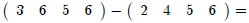
Example 12
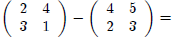
Scalar Multiplication: Given the scalar s, the scalar multiplication of sA
is
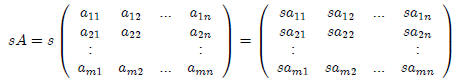
Matrix multiplication: If A is an m
× n matrix and B is a k × n matrix,
then their product C = AB is an m × n matrix where
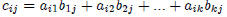
So
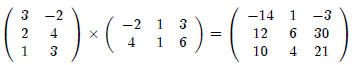
If
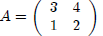and
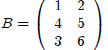then, BA =?
Note: the number of columns of the first matrix must equal the number of
rows of the second matrix. The size of the matrices (including the resulting
product) must be:
(m × k)(k × n) = (m × n)
Using matrix multiplication, we can now write the linear equation.
Let A be a m × n coefficient matrix
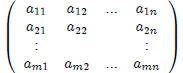
x be a m × 1 vector array of unknowns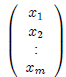
b be a m × 1 vector array of constants
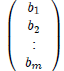
Then,
