Synthetic Division
1) (381:3)
Solve graphically.
x2 + 2y2 = 8
x − 2y = 4
2) (381:11)
Solve graphically.
x2 − 4y2 = 16
x2 + y2 = 1
3) (385:5)
Solve algebraically.
x + y = 1
x2− y2 = 1
4) (385:29)
A roof truss is in the shape of a right triangle.
If there are 4.60 m of lumber in the truss,
and the longest side (the hypotenuse) is
2.20m long, what are the lengths of the
other two sides of the truss?
5) (388:9)
Solve algebraically.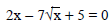
6) (388:27)
A rectangular TV screen has an area of 347 in2
and a diagonal of 27.0 in.
Find the dimensions of the screen.
7) (391:9)
Solve. 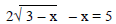
8) (391:23)
Solve. 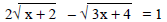
9) (391:37)
A freighter is 5.2 km farther from a Coast Guard
station on a straight coast than from the closest
point, A, on the coast. If the station is 8.3 km
from point A, how far is it from the freighter?
10) (397:15)
Find the remainder using the remainder theorem.
( x5 − 3x3 + 5x2 − 10x + 6 ) ÷ ( x − 2 )
11) (397:23)
Use the factor theorem to determine whether or
not the second expression is a factor of the first
expression.
x6 + 1, x + 1
12) (401:17)
Perform the indicated divisions by synthetic
division.
( x6 + 2x2 − 6 ) ÷ ( x − 2 )
13) (401:29)
Use the factor theorem and synthetic division
to determine whether or not the second
expression is a factor of the first.
2x4 − x3 + 2x2 − 3x + 1 ; 2x − 1
14) (405:5)
Solve using synthetic division, given the
root indicated.
2x3 + 11x2 + 20x + 12 = 0 ( r1 = −3/2 )
15) (405:21)
Solve using synthetic division, given the
root indicated.
x5 − 3x4 − x + 3 = 0 ( r1 = 3, r2 = j )
16) (411:15)
Solve without using a graphing calculator.
12x4 + 44x3 + 21x2 − 11x − 6 = 0
17) (411:31)
The deflection y of a beam at a horizontal
distance x from one end is given by
y = k( x4 − 2Lx3 + L3x ),
where L is the length of the beam and k is a constant.
For what values of x is the deflection zero?
18) (411:35)
For electrical resistors connected in parallel,
the reciprocal of the combined resistance equals
the sum of the reciprocals of the individual
resistances. If three resistors are connected in
parallel such that the second resistance is 1 ohm
more than the first and the third is 4 ohm more
than the first, find the resistance for a combined
resistance of 1 ohm.
19) (411:37)
A rectangular tray is made from a square piece
of sheet metal 10.0 cm on a side by cutting equal
squares from each corner, bending up the sides,
and then welding them together. How long is the
side of the square that must be cut if the volume
of the tray is 70.0 cm3?
20) (411:39)
The pressure difference p ( in kPa ) at a
distance x ( in km ) from one end of an oil
pipeline is given by
p = x5 − 3x4 − x2 + 7x .
If the pipeline is 4 km long, where is p = 0?
ANSWERS
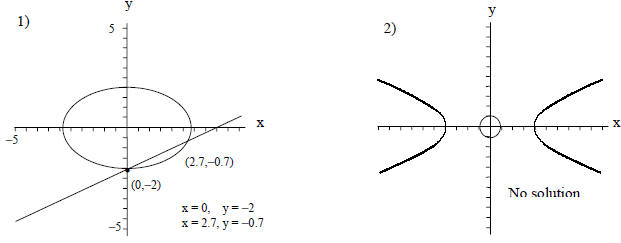
3) x = 1, y = 0
4) 2.19 m, 0.21 m
5) 1, 25/4
6) 15.9 in, 21.8 in
7) x = −1
8) x = 7, −1
9) 9.2 km
10) 14
11) no
12) x5 + 2x4 + 4x3 + 8x2 + 18x + 36, R = 66
13) yes
14) x = −2, −2
15) x = −j, −1, 1
16) x = 1/2, −2/3, −3, −1/2
17) x = 0, L
18) 2 Ω, 3 Ω, 6 Ω
19) 1.23 cm or 2.14 cm
20) x = 0.0 km, 1.6 km, 2.8 km


