Linear and Quadratic Equations Modulo Primes
DRAFT
In this lecture we discuss solving linear and quadratic equations modulo prime
p. To start, we
examine the simple linear case. In the quadratic case the problem is either
trivial or can be reduced
to finding square roots in Zp. From there we see that the square root can be
found in P or NP
depending on p. Finally, we describe a general algorithm for solving quadratic
equations mod p.
1 Linear Diophantine Equations
First, we study linear equations mod p.
Definition 1. A linear equation is an equation in the following form ax + by =
c.
Theorem 1. 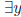 s.t. ax + ny = b
s.t. ax + ny = b
 ax ≡ b (mod n)
ax ≡ b (mod n)
Proof. A solution exists only if d = GCD(a, n)|b. If so, replace the equation by
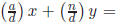
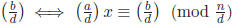 .
Thus,
.
Thus,
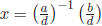 in
in
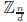
Example: 10x ≡ 6 (mod 12), GCD(10, 12) = 2. Then -x ≡ 5x ≡ 3 (mod 6), so x ≡
-3
≡ 3
(mod 6). The solutions mod 12 are x = 3 and x = 9.
2 Quadratic Equations
In this section we solve quadratic equations of the form ax2 + bx + c = 0 mod p.
We will assume
a=1 because we can always multiply the equation by a-1 ∈ Zp to put the equation
in the form
x2 + bx + c = 0. We consider the cases where p = 2 and p > 2 seperately.
2.1 Case p = 2
When p=2 there are only 4 possibilities for the equation so we simply list the
solutions:
| Equation | Factors | Roots |
| x2 = 0 | x · x | 0, 0 (double root) |
| x2 + x = 0 | x · (x + 1) | 0, 1 |
| x2 + 1 = 0 | (x + 1)2 | 1, 1 (double root) |
| x2 + x + 1 = 0 | irreducible in Z2[x] | none |
2.2 Case
p = odd prime
In this section we show that solving quadratic equations mod p can be reduced to
the problem of
finding square roots in Zp.
Theorem 2. The quadratic equation x2 + bx + c = 0 is solvable in
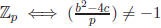 .
.
Proof. First, we derive the quadratic equation in Zp where a = 1:
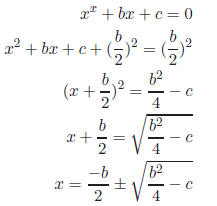
Then the theorem follows from the definition of the Legendre symbol:
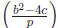 |
# of solutions |
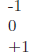 |
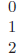 |
Note that when b2 - 4c ≡ 0 (mod p) then
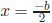 .
.
2.3 Finding square roots in Zp
Key Idea: To find 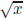 , express x = ye,
e even. Then
, express x = ye,
e even. Then 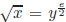 . We break this into additional
. We break this into additional
cases by considering p ∈ Z4.
| Case | |
|
p ≡ 0 (mod 4) p ≡ 1 (mod 4) p ≡ 2 (mod 4) p ≡ 3 (mod 4) |
Not possible Case 2.3.2 Trival case 2.1 Case 2.3.1 |
2.3.1 Case p ≡ 3 mod 4
In this section we use the fact that 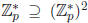 . Since
p is an odd prime
. Since
p is an odd prime 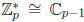 . Thus
. Thus
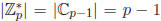 . Similarly,
. Similarly,
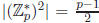 . Since p ≡ 3 (mod 4),
. Since p ≡ 3 (mod 4),
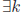 s.t. p = 4k + 3. Then
s.t. p = 4k + 3. Then
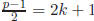 is also odd.
is also odd.
Theorem 3. In a finite abelian group G of odd order order,
squaring is onto.
Proof. Let 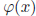 = x2 and show that given x ∈ G we can find y ∈ G s.t.
= x2 and show that given x ∈ G we can find y ∈ G s.t.
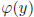 = x.
Let x ∈ G and
= x.
Let x ∈ G and
|G| = m = 2k + 1. Then 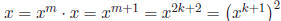 . So
. So
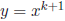 and
and 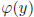 = x.
= x.
Theorem 4. In 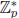 , if p ≡ 3 (mod 4) then
, if p ≡ 3 (mod 4) then
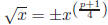 .
.
Proof. Recall that 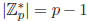 and
and
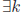 s.t. p = 4k
+3. Then
s.t. p = 4k
+3. Then 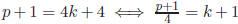 . By
. By
the previous theorem 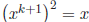 so
so
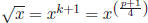 .
.
2.3.2 Case p ≡ 1 mod 4
To find ![]() in
in
![]() we will pick a t such that f(y) = y2 + ty + a is irreducible over Zp[y]. Fact:
f(y)
we will pick a t such that f(y) = y2 + ty + a is irreducible over Zp[y]. Fact:
f(y)
is irreducibly over 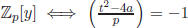 . We will show that ≈ 50% of t’s will work so we can
. We will show that ≈ 50% of t’s will work so we can
pick t uniformly random. We will work in the finite field F = Zp[y]/f(y) with p2
elements.
Definition 2. F has an automorphism given by
![]() = xp called the Frobenius
automorphism.
= xp called the Frobenius
automorphism.
Theorem 5. In F, 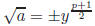
Proof. The roots of y2 + ty + a = 0 are y, yp. Thus yp+1 = a (in F) because p +
1 is even. Thus, if
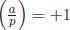 , we have
, we have 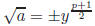 .
.
Example: Find 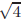 in Z5. Let a = 4. Then t2 - 4a = t2 - 16 = t2 - 1
in Z5. Let a = 4. Then t2 - 4a = t2 - 16 = t2 - 1
Choices for t
| t | t2 | t2 − 1 | Irreducible? |
| 0 | 0 | 4 | no |
| 1 | 1 | 0 | no |
| 2 | 4 | 3 | yes |
| 3 | 4 | 3 | yes |
| 4 | 1 | 9 | no |
Choose t = 2 for example. Then F = Z5[y]/(y2
+ 2y + 4). Then 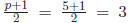 . So,
. So,
y3 = y · y2 = y(-2y -4) = y(3y +1) = 3y2 +4 = 3(3y +1)+y = (9y +y)+3 = 10y +3 =
3. Thus
32 ≡ 4 (mod 5). Also, (-3)2 = 22 = 4.
3 Next Time
Prove that ≈ 50% of t’s will work. Solve quadratic equations for arbitrary n.


