ACCUPLACER MATH REVIEW SHEETS
The Accuplacer exam is a branching exam. This means that when you miss a
problem, it will branch to a lower level
problem. When you get a problem right, the test then gives you a slightly more
difficult problem. In this fashion, this
test is very accurate in determining your placement into our DMAT/MATH program.
The first exam that you will be given will be the Elementary Algebra test.
Depending on your score, you will then take
either the Arithmetic (to place you into DMAT 0090, 0097, or 0098) or the
College- Level (to place you into DMAT
0099, or college level math classes).
If you have had two years or more of algebra in high school, it would be wise
to study all of the topics on this sheet.
However, if you did not have much algebra or feel very weak in algebra, you may
want to devote your time to studying
only the Arithmetic and Elementary Algebra Topics.
Arithmetic (17 questions)
I. Operations with whole numbers and fractions
A. Addition, Subtraction, Multiplication and division; Recognizing equivalent
fractions and mixed numbers
12. Change 42/16 to a mixed numeral.
13. Change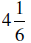
to an improper fraction.
B. Estimating
For #14 - 16: The World Almanac lists all 4-year colleges in the United
States with enrollments of 600 or more. This
list is 13 pages long, with an average of 89 colleges on a page.
14. Which figure best estimates the number of 4 year colleges listed? a. 157 b. 8000 c. 54000 d. 50 e. 1000
15. Estimate the minimum number of students enrolled at the colleges listed.
a. 54,000 b. 9000 c. 600,000
d. 5,400,000 e. 6,600,000
16. If you could compare the actual number of students attending 4-year
colleges to you estimate for question 15,
you estimate would turn out to be a. much higher b. a little higher c. much
lower d. a little lower e exactly
right.
II. Operations with decimals and percents
A. Addition, subtraction, Multiplication, division
B. Percent problems
21. What percent of 25 is 18?
22. What is 42% of 67? 23. 56 is 64% of what
number?
C. Recognition of decimal, percent, fraction equivalencies
24. Change 24% to a fraction in lowest terms.
25. Change 23.678 to a fraction in
lowest terms.
26. Change 3/4 to a percent.
27. Change 5/9 to a decimal.
28. Change 29.8% to
a decimal.
29. Change 0.0043 to a percent.
D. Problems involving estimation
30. Which is the least? a. 0.26, b. 0.026, c. 2.6 , d. 0.206
31. Junior earns $5.65 per hour that he works. If he worked 12 hours,
approximately how much did he earn?
a. $72 b. $60 c. $80
III. Applications and Problem Solving.
A. Rate, percent and measurement problems
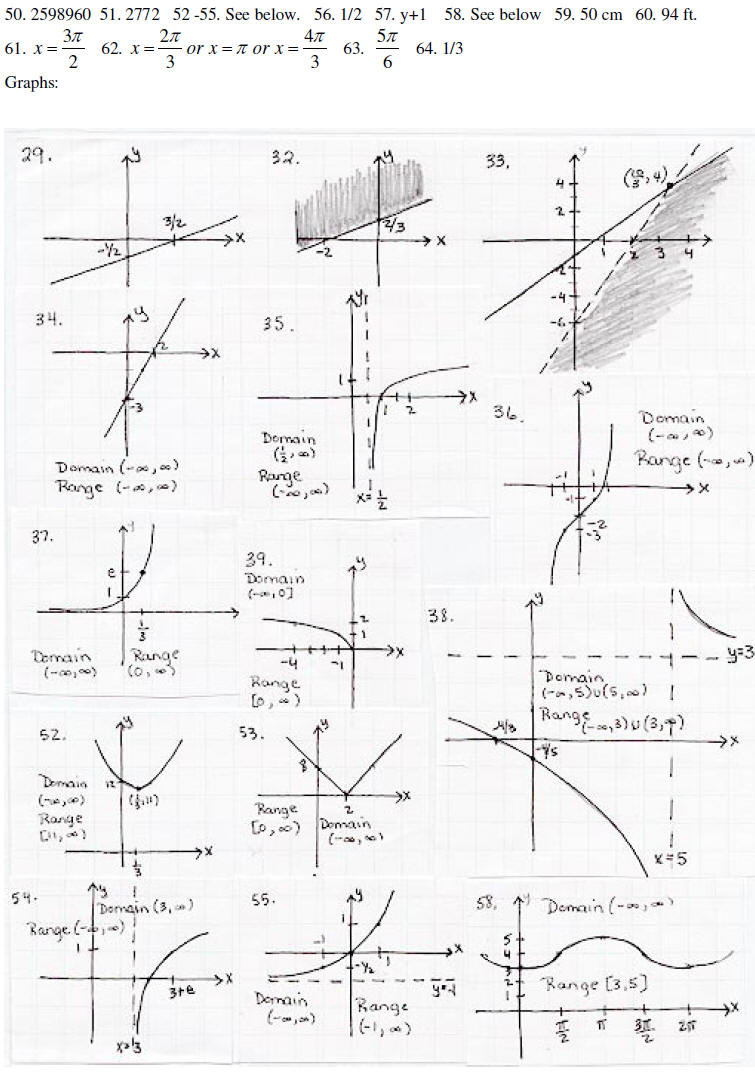
32. A soccer team played 160 games and lost 35% of them. How many games did they
lose?
33. A dieter lost 2 pounds in 3 weeks. If he continues to lose at this rate, how
many weeks will it take him to lose 24
pounds?
B. Simple geometry problems
34. Find the area of a square whose sides measure 4 cm.
35. Find the complement
of a 67° angle.
36. Find the perimeter of a triangle whose sides are 3m, 5 m, and 4 m.
37. If the legs of a right triangle measure 2 and 7, the hypotenuse measures
approximately
a. 7.28 b. 53 c. 14 d. 9.15 e. None of these
C. Distribution of a quantity into its fractional parts
38. Three people who work fulltime are to work together on a project, but their
total time on the project is to be
equivalent to that of only one person working full time. If one of the people is
budgeted for 1/2 of his time on the
project and a second person for 1/3 of her time, what part of the third worker's
time should be budgeted to this
project? a. 1/3 b. 1/4 c. 1/6 d. 1/8
Elementary Algebra (12 questions)
I. Operations with integers and rational numbers
A. Computation with integers and negative rational numbers
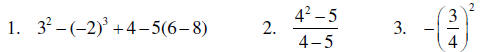
B. Use of absolute values and ordering
4. Put the following numbers in order
from least to greatest.
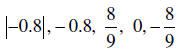
II. Operations with algebraic expressions
A. Evaluation of simple formulas and expressions
5. Evaluate I = Prt when P = 2000, r = 0.05, t = 3.
6. Evaluate xyz - 4 + 5x
when x = -1, y = 3, z = -2.
B. Addition, subtraction, multiplication, and division of monomials and
polynomials
Simplify the following expressions.
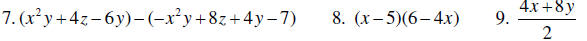
10. Perform the long division:
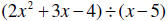
C. Evaluation of positive rational roots and exponents
11. Evaluate
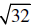
12. Simplify
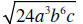
13. Simplify
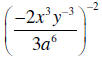
D. Simplify algebraic fractions
Simplify.
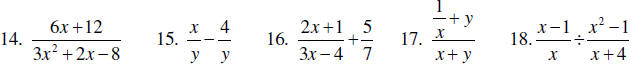
E. Factoring
Factor each expression
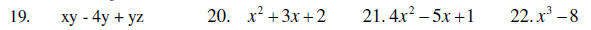
III. Solutions of equations, inequalities and word problems.
A. Solving linear equations and inequalities
23. Solve for x: 3x + 4 = -17 24. Solve: 4x - 7 < 8x + 4
B. Solutions of quadratic equations by factoring
25. Solve for x: x^2 + 4x + 3 = 0
C. Translating written phrases into algebraic expressions
26. Write the equation for the following : The sum of three consecutive odd
integers is 51. Do not solve.
27. Solve: The first angle of a triangle measures 2 times the sum of the second
and third angles. The second angle
measures 30° . Find the measure of the first angle.
D. Geometric reasoning and graphing
28. What quadrant is (9, -4) in? 29. Find the equation of the line passing
through (2,3) and (1,4) and graph.
College Level (20 questions)
I. Algebraic Operations
A. Simplifying rational algebraic expressions
Simplify each of the following expressions
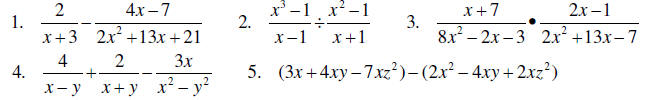
B. Factoring and expanding polynomials
6. Factor completely: 3x^4 -81xy^3 7. Multiply: (3x-5)(4x-1)
C. Manipulating roots and exponents
Simplify each of the following.
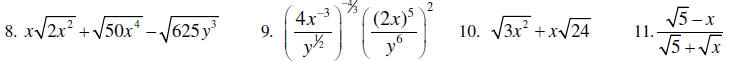
II. Solutions of equations and inequalities
A. Solution of linear and quadratic equations and inequalities
Solve each of the following.
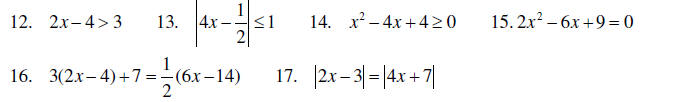
B. Systems of equations
Solve each system on the real numbers.
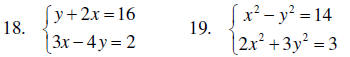
C. Other algebraic equations and inequalities
Solve each of the following equations and inequalities.
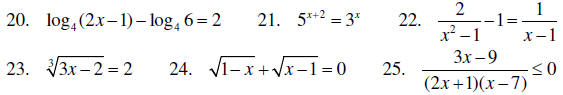
III. Coordinate geometry
A. Plane geometry
26. What quadrant is (3,-2) in? 27. Find the distance between (3,5) and (-2,
-6).
B. Straight line
28. Find the equation of the line perpendicular to 3x-y=7 that passes through
the point (-1,2).
29. Graph 2x – 6y = 3 30. Find the equation of the line passing through (2,9)
and (-1,-1).
C. Conics
31. Determine whether the following equations describe a parabola, a hyperbola,
an ellipse, a circle, or none of
these.
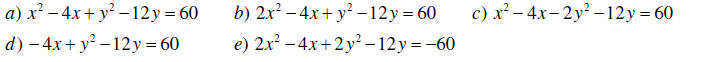
D. Sets of points in the plane
Graph the following inequalities and systems of inequalities.
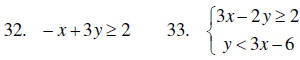
E. Graphs of algebraic functions
Graph the following functions. State the domain and range of each function.
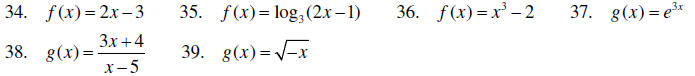
IV. Applications and other algebraic topics
A. Complex numbers
Simplify each of the following:
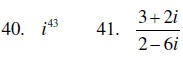
B. Series and sequences
Identify each series as arithmetic, geometric, or neither.
42. 1, 3, 5, 7, 9, ... 43. 1, -2, 4, -8, 16, -32, ... 44. 1, 1, 2, 3, 5, 8, 13,
...
45. Find the sum of the infinite geometric series: 1 + 1/2 + 1/4 + 1/8 + ...
C. Determinants, Permutations, Combinations, and Factorials, and Word
Problems
Evaluate:
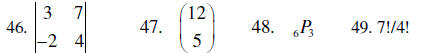
50. In a standard 52 card deck of playing cards, how many different ways can
a 5 card hand be chosen?
51. Out of a group of 15 people, where 4 are women and the rest are men, how
many ways can 2 women and 5
men be chosen?
V. Functions
A. Graphing polynomials, algebraic, logarithmic, and exponential functions
Graph each of the following and state the domain and range of each.
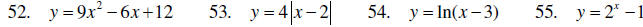
B. Evaluating polynomials, algebraic, logarithmic, and exponential functions;
Using properties of logs and
exponential to simplify expressions
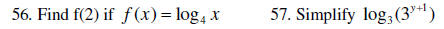
VI. Trigonometry
A. Graphing
58. Graph one period of y = 4 - cos x.
B. Word problems
59. A point P moves with angular velocity of 5 radians per second on a circle of
radius 2 cm. Find the distance
traveled by the point in 5 seconds.
60. From a point on the ground a person notices that a 75 foot antenna on the
top of a building has an angle of
elevation of 65° . If the angle of elevation to the top of the building is 50° ,
how tall is the building?
C. Solve trigonometric equations
Solve each equation exactly on the interval 0 ≤ x < 2π
.
61. 15sin x + 19 = 14sin x + 18
62. 2cos2x + 3cosx +1 = 0
D. Use inverse trigonometric functions
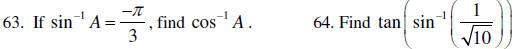
ANSWERS
ARITHMETIC TEST:
ELEMENTARY ALGEBRA TEST:
COLLEGE LEVEL TEST:
