Polynomial and Synthetic Division

 

Section 3.3 Objectives

• Use long division to divide polynomials by other
polynomials.
• Use synthetic division to divide polynomials by
binomials of the form (x – k).
• Use the Remainder Theorem and the Factor
Theorem.

Long Division

Find the quotient and remainder when
2x³ − 8x² + x − 4 is divided by 2x² −1

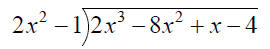
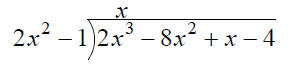
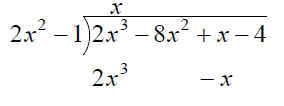
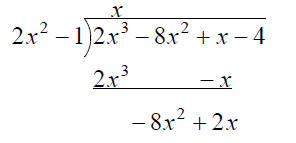
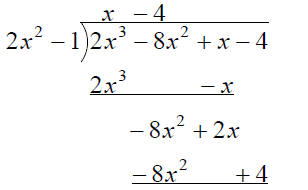
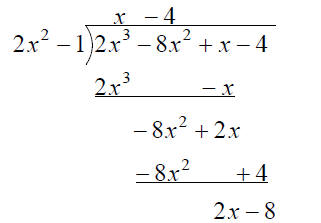
Check:

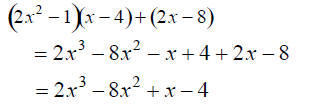
Thus,

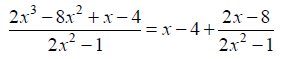
Division Algorithm for Polynomials

If f(x) and d(x) denote polynomial functions and if d(x) is
not the zero polynomial, then there are unique
polynomials q(x) and r(x) such that

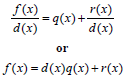
where r(x) is either the zero polynomial or a
polynomial of degree less than that of d(x). If the
remainder r(x) is zero, d(x) divides evenly into f(x).

Synthetic Division

Use synthetic division to find the quotient and
remainder when

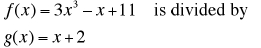
Coefficients of the dividend in descending powers of x are:

3 0 -1 11

Use the usual division sign and enter -2 in front of
it (since the divisor is x + 2)

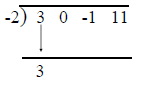
Multiply the latest entry in the bottom row by -2
and place the result in row 2 one column to the
right.

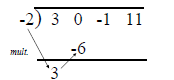
Add the last entry to the above number and enter
the sum into the bottom row.

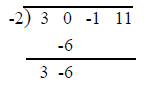
Repeat

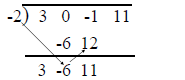
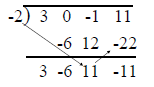
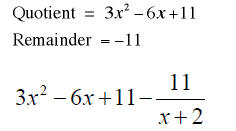
Remainder Theorem

Let f be a polynomial function. If f(x) is
divided by x - c, then the remainder is f(c).

Find the remainder if

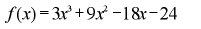
is divided by x + 3.

x + 3 = x - (-3)

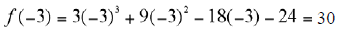
Factor Theorem

1. If f(c)=0, then x - c is a factor of f(x).
2. If x - c is a factor of f(x), then f(c)=0.

Use the Factor Theorem to determine whether the
function 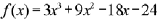has the factor

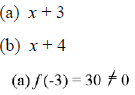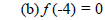x +3 is not a factor of f(x).

x + 4 is a factor of f(x).

What you should have learned

• Use long division to divide polynomials by other
polynomials.
• Use synthetic division to divide polynomials by
binomials of the form (x – k).
• Use the Remainder Theorem and the Factor
Theorem.