NUMBER SENSE: Factors of Whole Numbers
Having already found that GCF(30, 96) = 6, we could now
find
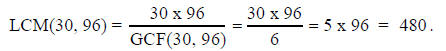
Explanation for this formula.
After recalling that GCF(24, 64) = 8, ask participants to
find
LCM(24, 64) by applying GCF(a, b) • LCM(â, b) using H-15.
LCM’s play an important role in the addition of fractions. In order to
add 1/12+ 3/8, we have to rewrite this problem in terms of equivalent
fractions with a common denominator.
One possible choice for a common denominator is 8 • 12,
leading to
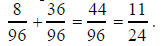
A more convenient choice is the least common denominator,
which is
LCM(12, 8) = 24. This leads to
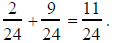
Have participants add fractions by finding least common
denominator
on worksheet H-16.
Practice word problems for LCM and GCF. Cover the answers.
In order to show that a given number is prime, it is
necessary to show
that its only factors are 1 and the number itself. For example,
The factors of 113 are: 1, 113
and for that reason 113 is prime.
Enrichment – Determining Whether a Number is Prime
A number that is a perfect square is surely not prime. Recalling that
the factors of all other non-prime numbers occur in pairs, it is not
necessary to check all smaller numbers as possible factors.
For example, to determine whether 137 is prime, we note
that 137 <
144, where 144 is a perfect square. For any pair of factors whose
product is 137, one of the factors would be less that
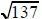. Since
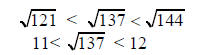
it is sufficient to confirm that the numbers 2, 3, 4, 5,
6, 7, 8, 9, 10, and
11 are not factors of 137. Having done this, we can conclude that 137
is prime.
In fact, it is not even necessary to check all whole
numbers between 1
and 11. If 6 were a factor of 137, its prime factors (notably 2 and 3)
would be factors of 137 as well. On this basis, we need only check
that the primes 2, 3, 5, 7, and 11 are not factors of 137.
More generally, to establish that a is prime, it is
sufficient to confirm
that all primes less than
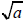fail to be factors of a.
Ask participants to determine whether the numbers 223 and
179 are
prime. What is the smallest list of numbers that must be checked as
possible factors of 223 and of 179?
Appendix
These slides give more detailed justification for the
rules for
determining divisibility by 2 and 3. The facilitator may use these
slides at his or her discretion. They may be used immediately
following slide T-6A.
Standards covered in this module:
| Grade 4 | Number Sense |
| 4.0 | 4.0 Students know how to factor small whole numbers. |
| 4.1 | 4.1 Understand that many whole numbers break down
in different way. |
| 4.2 | 4.2 Know that numbers such as 2, 3, 5, 7, and 11
do not have factors except 1 and themselves and that such numbers are called prime numbers. |
| Grade 5 | Number Sense |
| 1.4 | Determine the prime factors of all numbers
through 50 and write the numbers as the product of their prime factors using exponents to show multiples of a factor. |
| Grade 6 | Number Sense |
| 2.4 | Determine the least common multiple and greatest common divisor of whole numbers; use them to solve problems with fractions. |
Factors of Whole Numbers
Pre- Post-Test
1. List all the prime numbers less than 25:
2. Write the prime factorization for each number:
a. 30 =
b. 48 =
c. 37 =
d. 112 =
3. List all factors of
a) 30
b) 48
c) 37
d) 112
4. What is the greatest common factor of 48 and 112?
5. What is the least common multiple of 128 and 96?
6. State the Fundamental Theorem of Arithmetic.
Factors of Whole Numbers
Pre- Post-Test Answer Key
1. List all the prime numbers less than 25:
2, 3, 5, 7, 11, 13, 17, 19, 23
2. Write the prime factorization for each number:
a. 30 = 2 • 3 • 5
b. 48 = 2 • 2 • 2 • 2 • 3
= 24 • 3
c. 37 = 37
d. 112 = 2 • 2 • 2 • 2 • 7
= 24 • 7
3. List all factors of
a) 30 1, 2, 3, 5, 6, 10, 15, 30
b) 48 1, 2, 3, 4, 6, 8, 12 16, 24, 48
c) 37 1, 37
d) 112 1, 2, 4, 7, 8, 14, 16, 28, 56, 112
4. What is the greatest common factor of 48 and 112?
16
5. What is the least common multiple of 128 and 96?
384
6. State the Fundamental Theorem of Arithmetic
Every number has a unique prime factorization.
Divisibility
A whole number a is divisible by another
(smaller) counting number b if a = bq where q is
a whole number.
In this case we write a ÷ b = q
b is a factor or divisor of a
Example: a = 15 is divisible by b = 3
because 15 = 3q where q = 5
Equivalently, 15 ÷ 3 = 5
Notice that a = bq is a special case of a = bq + r
when r = 0. So a is divisible by b means that the
remainder is zero when a is divided by b.
Zero and One
Any whole number a is divisible by 1.
a ÷ 1 = a because a = 1 • a
0 is divisible by any number a ≠ 0
0 ÷ a = 0 because 0 = a • 0
Be careful!
0 • a = 0
means that you can divide a number into zero
What about dividing a number by zero?
a ÷ 0 does not make sense
suppose a ÷ 0 = q
then a = 0 • q
This is impossible if a ≠ 0.
If a = 0 then any value of q works,
but for division there can only be one answer.
Visualization of a = bq
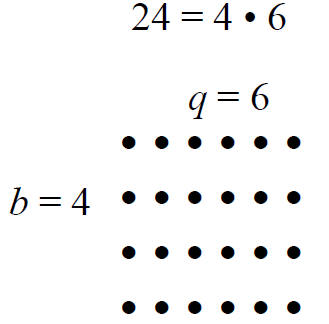
a) Is there another rectangular array
for 24?
b) How many arrays are there for 7?
Answer: For 7 there is only one array.
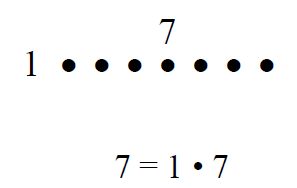b
ecause 7 is a “prime” number
A whole number is called prime if it has
exactly two factors,
One and itself.
The list of primes begins:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37,……..
There is no largest prime
A number > 1 that is not prime is called
composite