Math 111 Exam I Review

In class and on this review sheet, I will review some key points of the course so far. However, you
are expected to know ALL material that we have covered up to this point.

The Quick and Dirty Review

1. The Prologue

• Slopes of lines, solving equations involving lines.
• Solving quadratic equations and the quadratic formula .

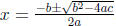2. Average (Overall) Rates of Change

• ATS (Car), Average (Overall) Output (Reservoir), AR and AC (Shin Polish), CGPA(Grade
Point), etc.

• The slope of the secant line through x = 0. If the graph goes through the point (0, 0),
then this is the slope of the diagonal line. The functional notation is 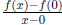. If f(0) = 0,
then .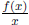

• Given a average (overall) rate of change, we draw a line through x = 0 with the given
rate (i.e. slope) and see where it intersects the graph.

3. Average (Incremental) Rates of Change

• As (Car), Average Change each half hour (Reservoir), MR and MC (Shin Polish), QGPA
(Grade Point), etc.
• The slope of the secant line from x = a to x = b. The functional notation is

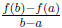
• Given an average (incremental) rate of change, we draw a reference through x = 0
with the given rate (i.e. slope) and slide our ruler parallel to this slope until we find an
appropriate interval.

4. Change in “Something”

• Change in Distance (Car), Change in Output (Reservoir), Change in TR and Change in
TC (Shin Polish), Change in Grade Points (Grade Point), etc.

• The change in height from x = a to x = b. The functional notation is f(b) − f(a)

• Recall, we often fix Δx = the change in x, and then we compute values of
Δf(x) = change in f(x)

5. Translation

• Be able to translate between the 3 languages: English, Graph, and Functional

6. Total Revenue (TR) and Total Cost (TC))

• Finding the quantity that gives biggest profit by looking at the TR and TC graphs.

• Finding the break even price (BEP) and shutdown price (SDP) and understanding
what these represent.

• Understand how profit, BEP, and SDP can be explored using MR, AC and AV C.

The More Elaborate Review

1. Prologue

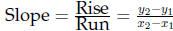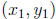• if and 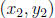are two points on the line. (Problems 1 - 6)

• Solving when lines intersect. (Problem 7)

• Quadratic equations, vertex formula, and the intersection of quadratics and lines. (Problems
8 - 11)

2. Worksheet 1 - The Car Story

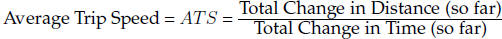• and Average Speed = AS


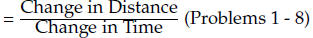
• Note that we fixed Δt = 5 and computed ΔD. The labeled C = the distance covered in a
five minute interval.

• ATS = slope of a secant through the  t = 0, AS = slope of a secant through t = a and
t = b. Note: We can use this to find the times that give lowest or highest ATS and AS.
(Problems 11-12, 1-I and 1-II)

3. Worksheet 2 - The Reservoir Story

• U(t) = usage over the last half hour, we computed O(t) = total output t hours after noon,
I(t) = total input t hours after noon. (Problems 1 - 4)

• Whenever input below output on the graph, there is a shortage. If we want to find the
least amount of water that has to be in the reservoir at noon we find the greatest distance
that output is above input. (Problems 5 - 8)

4. Worksheet 3 - The Print Shop Story

• TR = total revenue, TC = total cost, MR = marginal revenue = change in TR when
quantity q is increased by 1, MC = marginal cost. (Problems 1 - 7)

• P = profit = TR - TC, the quantity when TR has the greatest vertical distance above TC
is where profit is maximized. (Problems 8 - 11)

• Marginal Analysis: If MR > MC, then profit increases when we sell one more unit. If
MR < MC, then profit decreases when we sell one more unit. Profit is maximized at
the first quantity at which MR falls below MC. (Problems 12 - 14)

5. Worksheet 4 - Increments

• We discussed the similarities between the three stories and how there are total amounts
(D, O, and TR) and incremental amounts (C, U, and MR). (Problems 1 - 8, 4-I - 4-III)

6. Worksheet 5 - Increments and Speeds

• We noted how ATS in the car story corresponds to AR = average revenue = price in the
print shop story. We also noted how AS corresponds to MR. (Problems 1 - 7)

• The grade point story was introduced a another example. (Problems 8 - 15, 5-I)

7. Worksheet 6 - The Lagging Car

• Functional notation was introduced in this worksheet. We began the basic of translating
into functional notation. (Problems 1-13, 6-I)

8. Worksheet 7 - A Reservoir in Three Languages

• Translating between English, Graph, and Functional languages. (Problems 1 - 7, 7-I)

9. Worksheet 8 - Increments and Reference Lines

• This is an important section! We can answer 3 major questions by translating to graphical
language. (Problems 1, 2, 8-I - 8-III)

(a) Average (Overall) Rate of Change - Draw a line with the given slope through x = 0
and see where it intersects the graph. (Problem 3)

(b) Average Rate of Change over an Interval - Draw a reference line with the given slope
through x = 0 and slide the ruler parallel to the line until you find an interval of the
appropriate length. (Problems 4, 5, 7)

(c) Change in “Something” - Divide both sides by the length the the interval to get a
slope and proceed as in (b). (Problem 6)

10. Worksheet 9 - Analysis of Cost I

• FC = fixed cost (rent, etc.), V C = variable cost, TC = FC + V C.

• Given a market price p, we can draw a straight line graph for TR. The breakeven price
(BEP) is the slope of the lowest line through (0, 0) that crosses the TC graph. The
shutdown price (SDP) is the slope of the lowest line through (0, 0) that crosses the V C
graph. (Problems 1 - 14, 9-I)

– If p > BEP, then some quantities make a profit.
– If p < BEP, then no quantities make a profit
– If p > SDP, then some quantities will make more money than FC. (DON’T SHUT
DOWN)
– If p < SDP, then no quantities will make more money than FC. (SHUT DOWN)

11. Worksheet 10 - Analysis of Cost II

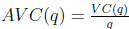• is the slope of the diagonal line through the graph of V C. (Problems 1 -
12, 10-I and 10-II)

• BEP = the intersection of MC and AC.

• SDP = the intersection of MC and AV C.