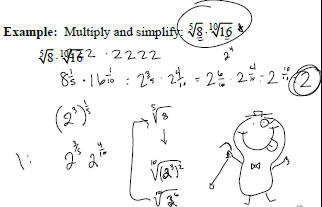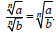Simplify Radical Expressions
7.3: Simplify Radical Expressions
Learning Objectives:
1. Use the product property to multiply
radical expressions.
2. Use the product property to simplify
radical expressions.
3. Use the quotient property to simplify
radical expressions.
4. Multiply radicals with unlike indices.
1. The Product Property
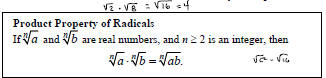
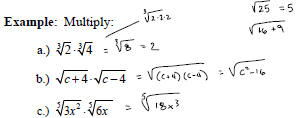
2. Simplifying Radical Expressions
A radical expression is simplified provided that the
radicand does not contain any factors that are perfect
powers of the index.
| Simplifying a Radical Expression
Step 1: Write each factor of the radicand as the
product Step 2: Write the radicand as the product of two Step 3: Take the nth root of each perfect power. |
Example: Simplify the following:
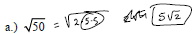
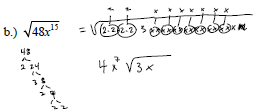
Example:
Simplify the following:
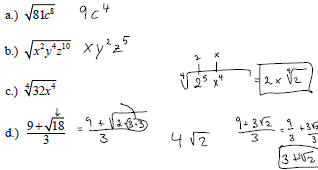
3. The Quotient Property
| Quotient Property of Radicals If 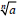 and and
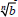 are real numbers, b ≠ 0, and n ≥ 2 is
an integer, are real numbers, b ≠ 0, and n ≥ 2 is
an integer,then
|
Example: Simplify: 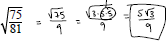
Simplifying Radical Expressions
Example: Simplify:
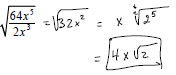
Example: Simplify:
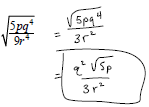
Example: Multiply and simplify.
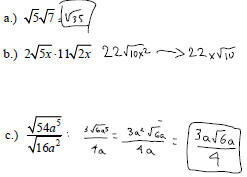
4. Multiplying with Unlike Indices