Derivative of the inverse of a function

Textbook pages 223-228
In some situations, a function is defined as the inverse of another function:
Examples:
•
•
•
•

When this is the case, to calculate the derivative those functions we use the inverse rule.
Rule:

Examples:
• Let f(x) = e^x, what is the derivative of ln(x) = f^-1(x) ?

• Let f(x) = arcsin(x), what is f'(x)?

• What is the derivative of arctan(x)?

Proof:

4.4.19 Derivatives of logarithmic functions

Textbook pages 229-231

A logarithmic function in base a, f(x) = log_a(x), is defined as the inverse of the expo-
nential function in base a. So, using the inverse rule we find that

Examples:

• The derivative of the natural logarithm is
• The derivative of log₂(x) is

Chain rule for logarithms: Given a function f(x), what is the derivative of ln[f(x)]?

Examples:
• f(x) = ln(3x + 1):
• f(x) = ln(sin(x)):

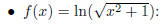
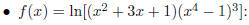
4.4.20 Logarithmic differentiation

Textbook pages 231-233

In the previous examples, we saw that taking the derivative of the logarithm of a com-
plicated function involving products and powers is actually very easy. By comparison, taking
the derivative of the function itself could be more complicated. Based upon this idea, we now
introduce the concept of logarithmic differfentiation. The following example will illustrate
how powerful this method is.

Example: Find the derivative of

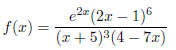
Idea:
• Take the logarithm of both sides of this equality, and expand the log.
• Take the derivative of both sides of this equality
• Multiply both sides by f(x) to obtain f'(x)

Example: The logarithmic differentiation is also useful to find derivatives of complicated
functions such as f(x) = x^x.

Proof of the power rule in the general case: Earlier in the lecture, we proved the
power rule

for positive integer vales of α. We are now able to prove it in the general case, using
logarithmic differentiation.

• Inverse Rule:
Using the inverse rule, find the derivative of f(x) = arccos(x).
• Derivatives of logarithmic functions
Textbook problems page 234 number 23, 27, 31, 33, 39, 43, 49
• Logarithmic differentiation:
– Let f(x) = g(x)^α. Using the chain rule, prove that 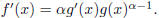Prove
the same result using logarithmic differentiation (i.e. say ln(f(x)) = ln(g(x)^α)
and take the derivative on both sides).
– Textbook problems page 234 number 63, 65, 67, 71, 73, 75.

• Miscellaneous derivatives problems
Textbook review problems page 243 number 1,3,5,7,15,23,30,36