Inverse Functions
4.1 Inverse Functions
I. Basic Concepts
A. Relation: a correspondence between two sets - a set of inputs called the
domain & a set
of outputs called the range.
B. Function: a special type of relation where every input has one and only one
output.
A function will pass a Vertical Line Test.
C. One-to-one Function: a special type of function where every input has one &
only one
output and every output has one & only one input. 1-1 functions pass a Vertical
Line Test
and a Horizontal Line Test.
D. The Inverse of a Function
Informal Definition: The inverse of a function undoes what the original function
did.
Formal Definition: Functions f and g are inverse functions if and only if
(f o g)( x) = f (g (x)) = x and (g o f) (x) = g (f (x)) = x.
Caution: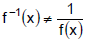 
f inverse does not equal 1
over f
II. Finding the Formula for the Inverse of a Function
Before you do anything else, determine if the given function is 1-1 by making an
accurate “quick
sketch” and then doing a VLT and a HLT. If the function is not 1-1, it does not
have an inverse.
If it is 1-1, find its inverse.
A. Finding an Inverse Algebraically
1. Replace f (x) with y.
2. Interchange x and y.
3. Solve for y.
4. Replace y with f -1(x).
Example 1
a. Sketch the graph of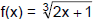 
and use the graph to determine whether
the function is 1-to-1.
Since the graph of f (x) passes both a vertical line test
and a horizontal line test, it is a 1-to-1 function and
it does have an inverse.
b. If the function is 1-to-1, algebraically find a formula for the inverse.
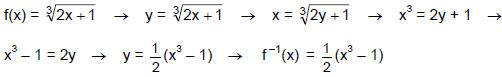
B. Finding an Inverse Informally
To undo what the original function did, the inverse function must do the
opposite
operations in the opposite order.
Example 2
Find the inverse of g (x) = 7x + 2 by thinking about the operations of the
function and then undoing them.
Check your work algebraically.
Since the graph of g (x) is an oblique line, it passes both a vertical and a
horizontal line test. Therefore g
does have an inverse.
Function g first multiplies x by 7 and second adds 2. To undo this, the inverse
function must
first subtract 2 and second divide by 7. Therefore,
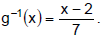
Check:
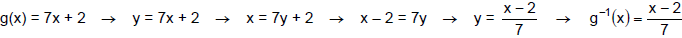
III. Characteristics of Inverse Functions
A. Only one-to-one functions have inverses.
B. The domain of f is the range of f -1 and the range of f is the domain of f -1.
C. If you make a t-chart for f and then use those y values as the x values to
make a t-chart
for f -1, the two t-charts will be mirror images of one another, i.e., their x
values and y
values will be reversed.
D. f and f -1 are symmetric around the y = x line.
E. If f and g are inverse functions, (f o g) (x) = f (g (x)) = x and (g o f) (x) =
g (f( x)) = x.
Example 3
Algebraically find the inverse of the given one-to-one function, f (x) = 3x2 – 5,
x ≥ 0.
Give the domain and range of f and f -1. Then graph f and f -1 on the same set
of axes.
Note: Without the restriction on the domain, f would not be a 1-to-1 function.
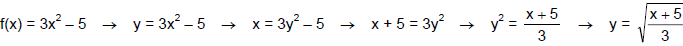
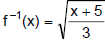
Note: Because of the restriction on the domain of f, x ≥ 0, f -1 has a
restriction
on its range, y ≥ 0, that is how we know the square root is positive and
not negative.
Domain of f = Range of f -1 = [0, ∞ ) and Range of f = Domain of f -1 = [–5, ∞ )
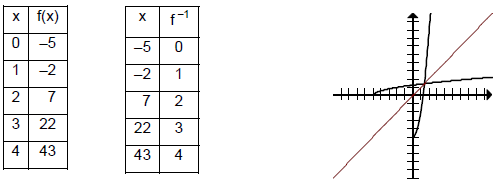
IV. Verifying Algebraically that Two Functions are
Inverses
If (f o f -1 )(x) = f (f -1(x)) = x and (f -1 o f )(x)= f -1(f(x)) = x, then f and
f -1 are inverse functions
Example 4
For the function f, use composition of functions to show that f -1 is as given.
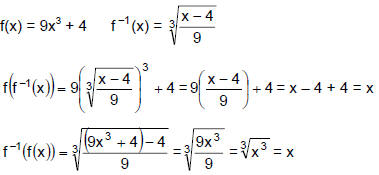
Since f (f -1(x)) = x and f -1(f(x)) = x, f and f -1 are inverse functions.