Fractions and Ratios

Goal	Description	Level	Lesson taught
8a	Use an algorithm to multiply mixed numbers	Beginning *does not need to be mastered	8.8

What this looks like:
There are two different ways to look at multiplying mixed numbers.

6 * 4 3/5

1. Partial Products. Calculate partial products and add.

a. Think of 4 3/5 as 4 + 3/5.	6 * 4 3/5	= 6 * (4 + 3/5)
b. Write the problem as the sum of partial products		= (6 * 4) + (6 * 3/5)
c. Calculate the partial products.		= 24 + 18/5
d. Convert 18/5 to a mixed number		= 24 + 3 3/5
e. Add		= 27 3/5

2. Improper Fractions: Convert whole numbers and mixed numbers to improper fractions.

a. Think: 6 = 6/1 and 4 3/5 = 23/5
b. Rewrite the problems	6 * 4 3/5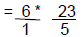
c. Use the algorithm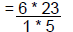
d. Multiply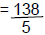
e. Covert to a mixed number		= 27 3/5

Like many of the algorithms with Everyday Mathematics, there is no “right” way. We encourage the students to use the one that works the best for them.

Goal	Description	Level	Lesson taught
8b	Use an algorithm to multiply fractions	Developing *does not need to be mastered	8.5-8.7 and 8.9

What this looks like:
Multiplying fractions is introduced through the use of area models. By using area models and proving problems like ¾ of ½ with the models, an algorithm is “discovered”.

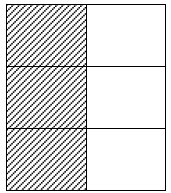
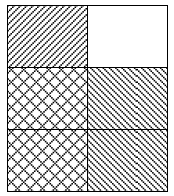
Area Model.
2/3 of ½

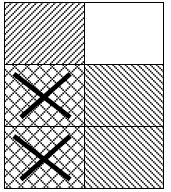The denominator of the second fraction is 2, so fold the paper in half. Shade ½.	The denominator of the first fraction is 3, so fold the paper in thirds horizontally	Open the sheet and shade the bottom 2/3 of the sheet.	Put an X in each of the 2 parts that were shaded twice. These parts represent 2/3 of ½ (2/6).

Algorithm.

Whole Number times Fraction

2/3 * 2		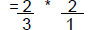Think of 2 as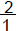
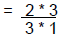		Apply the algorithm
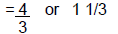		Solve.

Fraction times Fraction
Multiply the numerators together and the denominators together.

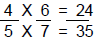
Goal	Description	Level	Lesson taught
8c	Use an algorithm to subtract mixed numbers with like denominators	Developing *does not need to be mastered	8.3

What this looks like:
When solving a subtraction problem with mixed numbers, it is critical that students understand how to rename mixed numbers and that they understand that renaming them does not change their value.

Goal	Description	Level	Lesson taught
8d	Find the percent of a number	Developing *does not need to be mastered	8.9-8.11

What this looks like:
There are several different approaches to finding the percent of a number. We encourage students to exercise their “percent sense” when approaching these problems. There is no one right way, and in general, different problems will be easier with different methods. Below are several methods for finding the answer to the same problem.

Example problem:
The flu hit Roosevelt School hard: 40% of the 480 students were absent at least one day last week. How many students were absent at least one day?

The unit-percent approach. 480 is 100% or the WHOLE
1% of 480 is 4.8
40 % is 40 X 4.8, or 192.

The 10-percent approach. 480 is 100% or the WHOLE.
10% of 480 is 48
40% is 4 X 48, or 192.

The equivalent-fraction approach. 40% is equal to 2/5.
40% is the same as 2/5 of 480 or 2/5 X 480, which is 192.

The equivalent-decimal approach. 40% is equal to 0.40.
40% is the same as 0.40 of 480 or 0.40 X 480, which is 192.

It is also good for students to understand the percents are really just special fraction with 100 as the denominator. Percent literally means “per 100”. So 45% is 45/100, 99% is 99/100, 7% is 7/100, and 100% is 100/100 or 1.

Many commonly used percents are equivalent to “easy” fractions: 25% = ¼, 50% = ½, and so on. IT may be easier to work with the easy fraction than with the fraction of a denominator of 100 when it is appropriate.

Goal	Description	Level	Lesson taught
8e	Use and algorithm to add mixed numbers	Developing/Secure *should show some level of mastery	8.2 & 8.4

What this looks like:
When adding mixed numbers whose denominators are the same, simply add the whole numbers and the fractions and simplify the answer if appropriate.

Example:

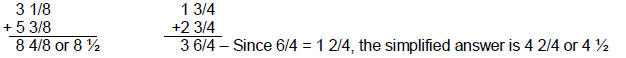
If the denominators of the fractions are not equivalent, then you have to convert one or both fractions to equivalent denominators before adding.

Example:

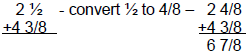
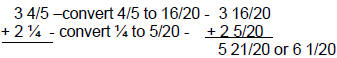
Goal	Description	Level	Lesson taught
8f	Order and Compare fractions	Developing/Secure *should show some level of mastery	8.1, 8.2, 8.12

What this looks like:
Students need to understand the relative sizes of fractions and need to be able to convert among equivalent fractions in order to make the comparisons. Sometimes they will be asked to compare two fractions, sometimes they will be asked to put three or more fractions in some sort of order.

Example:
In order to compare the fractions 4/5 and 7/8, you need to either be able to mentally see that 7/8 is bigger because its “missing piece” to get to one whole is smaller or you need to be able to convert both fractions to a common denominator – in this case 40. 40 is determined by multiplying 5 X 8.

Goal	Description	Level	Lesson taught
8g	Convert among fractions, decimals, and percents.	Secure *should be mastered by the test	8.8 & 8.9

What this looks like:
We have been practicing this skill throughout the year. The primary way that we work through the problems is by going from percent to fraction to decimal.

Example:
45% = 45/100 = 0.45
By putting the percent over 100, the decimal is easy to find.

Many of the “easy” fractions should be memorized. These include 50% = ½, 75% = ¾, 2/3 = 66 2/3%, 1/3 = 33 1/3%, 25% = ¼, 20% = 1/5, etc.

Goal	Description	Level	Lesson taught
8h	Convert between fractions and mixed or whole numbers	Secure *should be mastered by the test	8.2, 8.3, 8.8

What this looks like:

Fraction to Mixed Number/Whole Number
The numerator must be larger than the denominator. If this is the case, then divide the numerator by the denominator.

7/4 – 7 divided by 4 is 1 with a remainder of 3, therefore it is 1 ¾.
16/4 – 16 divided by 4 is 4 with no remainder, therefore it is 4.
25/6 – 25 divided by 6 is 4 with a remainder of 1, therefore it is 4 1/6.

Mixed Number to a Fraction.
You multiply the denominator by the whole number and then add the numerator. Use the original denominator in your answer.

4 1/3 – 3 X 4 = 12, 12 + 1 = 13, therefore the answer is 13/4
7 3/5 = 5 X 7 = 35, 35 + 3 = 38, therefore the answer is 38/5

There are times when the students are given two mixed numbers are asked to figure out a missing number. They have to use their knowledge of fractions to figure out the missing number.

Example:
5 ¾ = 4 ?/4. Since the whole number went from 5 to 4, 4/4 or 1 were added to the fraction. Therefore you would add 4/4 to the ¾ that were given for a total of 7/4. So the ?=7.

Goal	Description	Level	Lesson taught
8i	Find Common Denominators	Secure *should be mastered by the test	8.1, 8.2, 8.4, 8.12

What this looks like
If the smaller denominator goes into the larger denominator, then use the larger denominator as the common denominator. For example – ¾ and ½ - Since 2 goes into 4, use 4 as the CD converting ½ into 2/4.

If the smaller denominator does not go into the larger denominator, then multiply the two denominators together to find a CD. For example – 2/3 and 3/5 – multiply 3 X 5 to 15 as the CD. So 2/3 becomes 10/15 and 3/5 becomes 9/15.

See Goal 8f for an example of how to do the actual conversions.