Classification and Linear Equations
Example. Find the general solution to
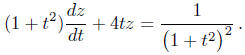
Solution. First bring the equation into the normal form
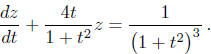
An integrating factor is
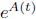 where A′(t) = 4t/(1 + t2).
Setting
where A′(t) = 4t/(1 + t2).
Setting
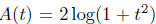 , we
, we
see that
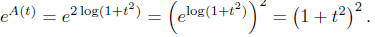
We then bring the differential equation into the integrating factor form
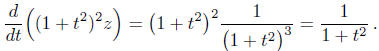
By integrating both sides of this equation we obtain
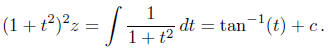
The general solution is therefore given by
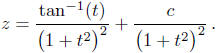
2.3.2. Homogeneous Linear Equations. The linear equation
(2.8) is said to be homogeneous
when r(t) = 0 for every t, and is said to be inhomogeneous otherwise. When (2.8)
is
homogeneous its normal form (2.9) is simply
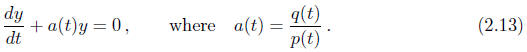
By formula (2.12) its general solution is simply
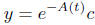 where A′(t) = a(t) and
c is any constant . (2.14)
where A′(t) = a(t) and
c is any constant . (2.14)
Hence, for homogenous linear equations the recipe for
solution only requires finding one
primitive — namely, a primitive of a(t). This means that for simply enough a(t)
you
should be able to write down general solutions immediately.
Example. Find the general solution to
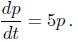
Solution. Because a(t) = −5, a general solution is
given by
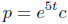 , where c is an arbitrary constant .
, where c is an arbitrary constant .
Example. Find the general solution to
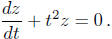
Solution. Because a(t) = t2, a general solution is given by
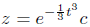 where c is an
arbitrary constant .
where c is an
arbitrary constant .
2.3.3. Initial-Value Problems for Linear Equations. In
order to pick a unique solution
from the family (2.12) one must impose an additional condition that determines
c. We do
this by again imposing an initial condition of the form
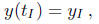
where
![]() is called the initial
time and
is called the initial
time and
![]() is called the initial
value or initial datum. The
is called the initial
value or initial datum. The
combination of the differential equation (2.9) with the above initial condition
is
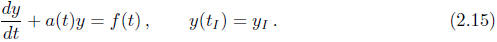
This is a so-called an initial-value problem. By imposing
the initial condition upon the
family (2.12) we see that
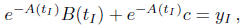
which implies that 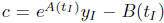 .
Therefore, if the primitives A(t) and B(t) exist
.
Therefore, if the primitives A(t) and B(t) exist
then the unique solution of initial-value problem (2.15) is given by
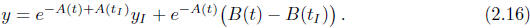
2.3.4. Existence of Solutions for Linear Equations. Even
when you cannot find primitives
A(t) and B(t) analytically, you can show that a solution exists by appealing to
the Second
Fundamental Theorem of Calculus whenever a(t) and f(t) are continuous over an
interval
![]() that contains the
initial time
that contains the
initial time ![]() . In
that case one can express A(t) and B(t) as
. In
that case one can express A(t) and B(t) as
the definite integrals
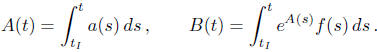
For this choice of A(t) and B(t) one has
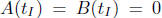 , whereby formula (2.16)
, whereby formula (2.16)
becomes
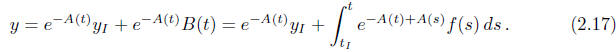
The First Fundamental Theorem of Calculus implies that
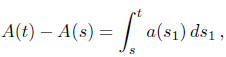
whereby formula (2.17) can be expressed as
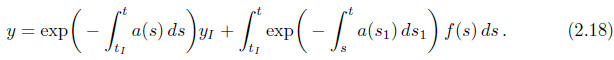
This shows that if a and f are continuous over an interval
![]() that contains
that contains
![]() then the
then the
initial-value problem (2.15) has a unique solution over ![]() ,
which is given by formula
,
which is given by formula
(2.18).
For linear equations one can usually identify the interval of existence for the
solution
of the initial-value problem (2.15) by simply looking at a(t) and f(t).
Specifically, if Y (t) is
the solution of the initial value problem (2.15) then its interval of existence
will be ![]()
whenever:
• the coefficient a(t) and forcing f(t) are continuous over ![]() ,
,
• the initial time ![]() is
in
is
in ![]() ,
,
• either the coefficient a(t) or the forcing f(t) is not defined at both
![]() and
and
![]() .
.
This is because the first two bullets along with the formula (2.18) imply that
the interval
of existence will be at least ![]() ,
while the last two bullets along with our definition
,
while the last two bullets along with our definition
(2.2) of solution imply that the interval of existence can be no bigger than
![]() because
because
the equation breaks down at
![]() and
and
![]() . This argument works
when
. This argument works
when
![]() or
or
![]() .
.
Example: Give the interval of existence for the solution of the
initial-value problem
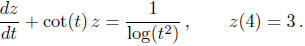
Solution: The coefficient cot(t) is not defined at
t = nπ where n is any integer, and is
continuous everywhere else. The forcing 1/ log(t2) is not defined at
t = 0 and t = 1, and
is continuous everywhere else. The interval of existence is therefore ( π, 2π )
because: both
cot(t) and 1/ log(t2) are continuous over this interval; the initial
time is t = 4, which is in
this interval; cot(t) is not defined at t =π and t = 2π .
Example: Give the interval of existence for the solution of the
initial-value problem
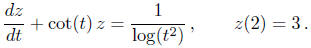
Solution: The interval of existence is (1,π)
because: both cot(t) and 1/ log(t2) are con-
tinuous over this interval; the initial time is t = 2, which is in this
interval; cot(t) is not
defined at t =π while 1/ log(t2) is not defined at t = 1.
Remark: If y = Y (t) is a solution of (2.15) whose interval of existence
is ![]() then
then
this does not mean that Y (t) will become singular at either
![]() or
or
![]() when those
when those
endpoints are finite. For example, y = t4 solves the initial-value
problem
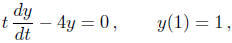
and is defined for every t. However, the interval of
existence is just (0,∞) because the
initial time is t = 1 and normal form of the equation is
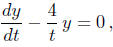
the coefficient of which is undefined at t = 0.
Remark: It is natural to ask why we do not extend our definition of
solutions so that
y = t4 is considered a solution of the initial-value problem
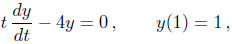
for every t. For example, we might say that y = Y (t) is a
solution provided it is differ-
entiable and satisfies the above equation rather than its normal form. However
by this
definition the function
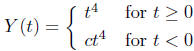
also solves the initial-value problem for any c. This
shows that because the equation breaks
down at t = 0, there are many ways to extend the solution y = t4 to t
< 0. We avoid such
complications by requiring the normal form of the equation to be defined.


