Fractions, Ratios, Money, Decimals and Percent
Teacher: Find the areas for all the geoboard triangles that you can, even the
ones that are not
right triangles. Record their bases, heights and areas. Prove the areas that you
find.
The rule is that the base for each triangle that you make has to be on the
bottom row of nails.
(illustration 11-2-8)
(Several triangles on geoboards and recorded on paper. With their bases, heights
and areas recorded in a
table.)
The bases must be on the bottom row of the geoboards because measuring triangles
made another way
is more difficult. Which side of the triangle below shall we say is the base?
What might be its height?
What might be the measurements for each?
(illustration 11-2-9)
(Show a triangle on a geoboard with no sides parallel to the bottom row and no
side lengths easily
counted by nails touched.)
Mathematics is simple and basic and straightforward. The rules we add are
designed to keep it so.
Teacher: Can you find a pattern in the areas of your triangles that might
help you predict the
areas for all triangles?
Is the pattern you find now anything like the pattern you found for right
triangles?
Four triangles...
Teacher: Here are four triangles I have made.
(illustration 11-2-10)
(First triangle: Right triangle with a base of one and a height of four. The
base extends from the first to
the second nail of the bottom row. The height extends from the second nail of
the bottom row to the
second nail of the top row. The second triangle is exactly the same as the first
except that the top of the
triangle is now the third nail of the top row. The third triangle is exactly the
same as the second except
that the top of the triangle is now the fourth nail of the top row. The fourth
triangle is exactly the same
as the first except that the top of the triangle is now the fifth nail of the
top row.)
Teacher: What is the base of each of these triangles?
Students: One.
Teacher: What is the height of each of these triangles?
Students: Four.
Teacher: What are the areas of each of these triangles? Work with a partner to
find out.
Is there a pattern to be seen?
Our students learn...
When we ask our students to prove the areas of shapes on their geoboards, our
students learn to use
their problem-solving skills. They learn to find areas and prove the areas that
they find. They learn
from one another a variety of approaches to discovering new solutions. They
learn from us techniques
than might not occur to them. They learn that there are patterns in the answers
to our questions. They
also learn that using fractions at school is as easy and as natural as cutting
cake at home.
Lesson Three
| Purpose | Learn that fractions are special numbers
describing part/whole relationships. Learn to add and subtract simple fractions. |
| Summary | Students learn to use people in the room to
create simple fractions, then addition and subtraction problems. They also learn to create stories to accompany fractional numbers. |
| Materials | Students in the room, chalkboards, paper. |
| Topic | Fractions are created with people in the class. |
| Topic | Students create their own addition problems. |
| Topic | Students create their own subtraction problems. |
| Homework | What problems can our students create with the
people in their home? |
People fractions...
Teacher: How many people are in our class today? Count all the students in the
room. Count me
in as well.
Students: Thirty.
Teacher: What fraction of the people in the room are each of you?
The thirty in the answer given by the students represents the thirty people in
the room, or the whole.
But fractional numbers represent two different concepts at once—the whole and
the part.
Teacher: Altogether, we are one whole class. The fraction of the class we are
is the part we are of
the whole. Thirty people are in the room. I am one of them. So, I am
one-thirtieth of the
people in the room. One out of thirty, or one-thirtieth, is written one over
thirty, like this:
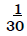
What fraction of the people in the room are you?
When the students know what fraction, or part, of the class they are, the
teacher changes what is called
the whole and asks again.
Teacher: Now, your row is one whole row.
How many people are there in your row?
What fraction of your row are you?
Use your chalkboards to show me how you think you write the fraction that you
are.
Easy to say...
Eventually, our students will have to know the formal names for every fraction
that they say or write:
one over seven is one-seventh; one over two is one-half. But eventually does not
mean right now. We
can start our students out with fractions that are easy to say and easy to
write.
Parts and wholes are not difficult to write. The number on the bottom (the
denominator) is the number
of the whole. The number on the top (the numerator) is the number for the parts.
If we read the fraction
as parts over wholes, parts and wholes are not difficult to say. One-eighth, one
out of eight, or one over
eight—if our students understand the meaning of the fraction, we accept anyway
they say it at the start.
Adding people fractions...
Teacher: I am going to make up an addition problem for fractions. Cindy, how
many people are in
your row?
Student: Seven.
Teacher: What fraction of your row are you?
Student: One out of seven.
Teacher: How would you write that?
Student: One over seven.
Teacher: Show me on your chalkboard, please.
Student: 1/7
Teacher: What fraction of your row is Nicole?
Student: She's one over seven, too.
Teacher: What fraction of your row are you and Nicole together?
Student: Two over seven.
Teacher: We would write the addition problem like this:
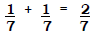
Teacher: Now, everyone write this next problem that I
make up on your individual chalkboards.
What fraction of his row is Daniel? Don't tell me. Write the fraction for Daniel
on your boards.
What fraction of Daniel's row is Michael? Write that on your boards next to the
Daniel fraction
already there, with a plus sign between.
Now, what fraction of Daniel's row are Daniel and Michael together? Write that
on your boards.
Don't forget to put the equals sign where you think it goes. Hold up your boards
so I can see
what you have written.
The students record fraction problems on their individual chalkboards until the
teacher feels they
understand the process well enough to begin creating fraction problems on their
own.
Teacher: Now, I want you to make up your own fraction problems for people.
You may work
together or by yourself. You may write about the people in the room or people
from any other
place you wish.
For each problem you create, please say what the whole group is before you write
the fractions.
Then either write a story or draw a picture to go along with the problems you
create.
Our assessment...
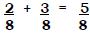
Teacher: Who can give me a story to go along with these
numbers?
When we tell our students to write the numbers for our problems, our assessment
of our students'
understanding is in the numbers that they write. When we ask our students to
create problems on
their own, our assessment is in the words and pictures that they write or draw.
Our assessment of our
students' understanding of the numbers that we write is in the stories they
create.
As we do for all number operations, we connect concepts to symbols.
Concept-connecting-symbolic
means we use symbols to record events. Symbolic-connecting-concept, means we
start with the
symbols and construct what the symbols represent. Concept-connecting-symbolic,
symbolicconnecting-
concept—two-way street.
Teacher: Why is the answer to the 2/8 + 3/8 problem 5/8 and not 5/16? Why
don't we add the
bottom numbers to each other just like we add the top?
Can our students explain why we add numerators and not denominators? Is it
possible for students to
discover the rules for fractions for themselves?
Teacher: If a new child were to come to our class today, could you explain to
him or her the rules
for adding fractions? What do you think you might say?
Can our students verbalize or write out the knowledge that they have?
Subtracting-people fractions...
Teacher: How many people are in Brenda's row?
Students: Six.
Teacher: Brenda, Anthony and Russell, please stand up.
Teacher: What fraction of Brenda's row is standing up?
Students: Three out of six.
Teacher: Show me on your chalkboards, please.
Students: 3/6
Teacher: I'll write that on the overhead.
Three-sixths or three over six is the starting number in my subtraction problem.
Anthony and
Russell, please sit down.
What fraction of the row did I have sit down? Please write it on your
chalkboards next to the
three-sixths. Show me what you have.
Students: 3/6 2/6
Teacher: Put a minus sign in front of the two-sixths, so we can tell it is the
number to be taken
away. Show me what you have on your boards now.
Students: 3/6 - 2/6
Teacher: I'll write that on the overhead, as well.
What is the answer to this subtraction problem? What fraction of Brenda's row is
still left
standing after Russell and Anthony sat down? Write the fraction on your boards.
Don't
forget the equals sign.
Students: 3/6 - 2/6 = 1/6
The students record the fraction problems for subtraction on their individual
chalkboards until the
teacher feels they understand the process well enough to begin creating problems
for themselves.
Teacher: Now, I want you to make up your own fraction problems for people.
You may work
together or by yourself. You may write about the people in the room or people
from any other
place you wish. You may make up subtraction problems or addition problems or
problems that
have addition and subtraction mixed in.
Please say what the whole group is before you write the fractions. You may
either write a story
or draw a picture to go along with each problem you create.
Let people help...
Fractions are special numbers that represent two concepts at once—the whole and
the part. Students
who are old enough to know that they are individuals at the same time that they
are part of a whole
group, are old enough to understand what people fractions mean.
Unless we are alone, we are in a group. We can ask people-fraction questions
standing in the lunch
line, waiting for the school bus, or sitting in a row of seats impatient for the
assembly to begin. Peoplefraction
questions can go home. What fraction of each family is each child? What fraction
of each
family is girls? What fraction is boys? What other people-fraction questions can
our students ask at
home? People fractions follow us wherever we go.
Learning about fractions is not something we save for an upper grade. We use
Power Blocks and
geoboards to help us make fractions a natural part of our students' learning
from their earliest years in
school. We let people help us, too.


