Math 037 Homework 4 Solutions

Section 3.1

3.a. Yes. Let k = 2rs. Since r and s are integers, so it k. Now 4rs = 2(2rs) = 2k. Thus, by the
definition of even, 4rs is even.

b. Yes. Let k = 3r+2s^2+1. Since r and s are integers, so is k. Now 6r+4s^2+3 = 2(3r+2s^2+1)+1 =
2k + 1. Thus, by the definition of odd, 6r + 4s^2 + 3 is odd.

c. Yes. We know r^2 +2rs+s^2 = (r +s)(r +s). Since r and s are both positive integers, r +s must
be a positive integer greater than 1. Thus, we have written r^2 + 2rs + s^2 as the product of two
positive integers greater than 1. Thus, r^2 + 2rs + s^2 is composite by the definition of composite.

6. Let a = b = 0. Then a and b are real numbers such that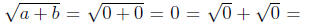

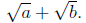
12. Let n = 9. Then n is odd, but (n - 1)/2 = 4 is even.

16. This property is sometimes true and sometimes not true. For example, it is true for the pair 7
and 11. It is not true for the pair 7 and 9.

28. Thm: 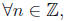is n is odd, then n^2 is odd.

Proof: Let n be any odd integer. Then, from the definition of odd, there is an integer k such that
n = 2k +1.Let k₁ = 2k^2 +2k. Since k is an integer, so is k₁. Now, n^2 = (2k +1)^2 = 4k^2 +4k +1 =
2(2k^2 + 2k) + 1 = 2k₁ + 1 for some integer k₁. Thus, by the definition of odd, n^2 is odd.

46. Thm: 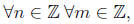if n - m is even, then n^3 - m^3 is even.
Proof: Let n and m be integers such that n - m is even. Thus, by the definition of even, there
exists an integer k such that n-m = 2k. Let k₁ = k(n^2 +nm+m^2). Since k, n, and m are integers,
so is  k₁. Now, n^3 - m^3 = (n - m)(n^2 + nm + m^2) = 2k(n^2 + nm + m^2) = 2 k₁, for some integer  k₁.
Thus, by the definition of even, n^3 = m^3 is even.

48. This is false. Let m = 3. Note m is an integer but m^2 - 4 = 5 is prime.

53. This is false. Let m = 8 and n = 2. Then m and n are both positive integers and mn = 16
which is a perfect square, but neither m nor n is a perfect square.

54. Thm: The difference of the squares of any two consecutive integers is odd.
Proof: Let n and n + 1 be any two consecutive integers. Then the difference of their squares can
be written as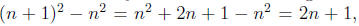where n is an integer. Thus, from the
definition of odd, the difference of the squares of any two consecutive numbers is odd.

Section 3.2

7. 5246197/99990

8. a. 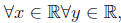if xy = 0, then x = 0 or y = 0.

c. There exist a pair of nonzero real numbers x and y such that their product is zero.

17. Thm: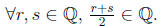

Proof: Let r and s be rational numbers. Then, from the definition of rational numbers, there exist
integers a, b, c, d such that b ≠ 0, d ≠ 0, r = a/b and s = c/d. Let A = ad + bc and B = 2bd. Since
a, b, c, d are integers, so are A and B. Since neither b nor d are zero, neither is B.

Now,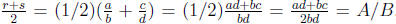where A and B are integers and B is not
zero. Thus, by the definition of a rational number, (r + s)/2 is rational.

19. Thm: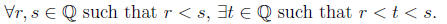

Proof: Let r and s be any two rational numbers. From #17, the number t = (r + s)/2 is also a
rational number. From #18, r < t < s. Thus, between any two distinct rational numbers, there
exists a rational number strictly between them.

Section 3.3

3. yes. Pick k = 0, Now, 3 * k = 3 * 0 = 0.

9. yes. We know that 2a * 34b = 4 * 17ab. Since a and b are integers, so is 17ab. So 4|(2a * 34b) by
the definition of divisibility. So 4 is a factor of 2a * 34b.

16. Thm: For all integers a, b, and c, if a|b and a|c, then a|(b - c).
Proof: Let a, b, and c be integers such that a|b and a|c. Thus, by the definition of divisibility, there
exist integers k₁ and k₂ such that ak₁ = b and ak₂ = c. Let k₃ = k₁ - k₂. Note that since k₁ and k₂
are integers, so is k₃. Now, b - c = ak₁ - ak₂ = a(k₁ - k₂) = ak₃ where k₃ is an integer. Thus, by
the definition of divisibility, a |(b - c).

20. Thm: If an integer n is divisible by 16, then n is divisible by 8.

Proof: Let n be an integer that is divisible by 16. Then, by the definition of divisibility, there
exists an integer k such that n = 16k. Let k₁ = 2k.Since k is an integer, so is k₁. Now,
n = 16k = 8(2k) = 8k₁ where k₁ is an integer. Thus, by the definition of divisibility, n is divisibly by 8.

25. This is not true. Let a = 6, b = 2, and c = 3. Then