Sums and Differences of Rational Functions

Equivalent Fractions

If you slice a pizza into four equal pieces, then consume two of the four slices, you’ve
consumed half of the pizza. This motivates the fact that

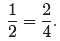
Indeed, if you slice the pizza into six equal pieces, then consume three slices, you’ve
consumed half of the pizza, so it’s fair to say that 3/6 = 1/2. Indeed, all of the following
fractions are equivalent:

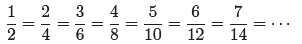
A more formal way to demonstrate that 1/2 and 7/14 are equal is to start with the
fact that 1/2 = 1/2 × 1, then replace 1 with 7/7 and multiply.

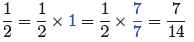
Here’s another example of this principle in action, only this time we replace 1 with
(x − 2)/(x − 2).

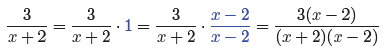
In the next example we replace 1 with (x(x − 3))/(x(x − 3)).

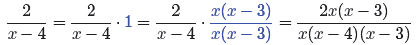
Now, let’s apply the concept of equivalent fractions to add and subtract fractions
with different denominators.

Adding and Subtracting Fractions with Different Denominators

In this section we show our readers how to add and subtract fractions having different
denominators. For example, suppose we are asked to add the following fractions.

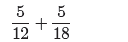(8)

First, we must find a “common denominator.” Fortunately, the machinery to find
the “common denominator” is already in place. It turns out that the least common
denominator for 12 and 18 is the least common multiple of 12 and 18.

18 = 2 · 3²
12 = 2² · 3
LCD(12, 18) = 2² · 3² = 36

The next step is to create equivalent fractions using the LCD as the denominator.
So, in the case of 5/12,

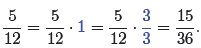
In the case of 5/18,

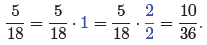
If we replace the fractions in equation (8) with their equivalent fractions, we can
then add the numerators and divide by the common denominator, as in

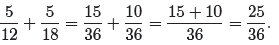
Let’s examine a method of organizing the work that is more compact. Consider the
following arrangement, where we’ve used color to highlight the form of 1 required to
convert the fractions to equivalent fractions with a common denominator of 36.

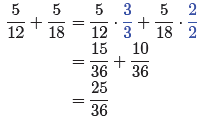
Let’s look at a more complicated example.

→ Example 9. Simplify the expression

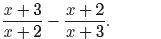(10)

State all restrictions.

The denominators are already factored. If we take each factor that appears to the
highest exponential power that appears, our least common denominator is (x+2)(x+3).
Our first task is to make equivalent fractions having this common denominator.

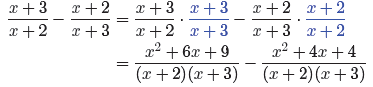
Now, subtract the numerators and divide by the common denominator.

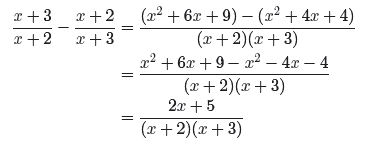
Note the use of parentheses when we subtracted the numerators. Note further how the
minus sign negates each term in the parenthetical expression that follows the minus
sign.

Tip 11. Always use grouping symbols when subtracting the numerators of fractions.

In the final answer, the factors x + 2 and x + 3 in the denominator are zero when
x = −2 or x = −3. These are the restrictions. No other denominators, in the original
problem or in the body of our work, provide additional restrictions.

Thus, for all values of x, except the restricted values −2 and −3, the left-hand side
of

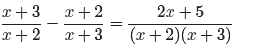(12)

is identical to the right-hand side. This claim is easily tested on the graphing calculator
which is evidenced in the sequence of screen captures in Figure 2. Note the ERR (error)
message at each restricted value of x in Figure 2(c), but also note the agreement of
Y1 and Y2 for all other values of x.

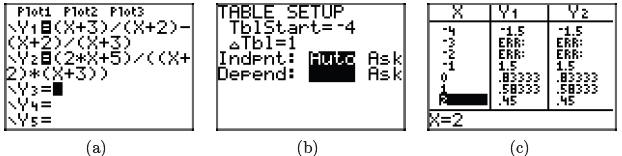
Figure 2. Using the table feature of the graphing calculator to check the result in
equation (12).

Let’s look at another example.