Units, Measurement, Dimension

Dimension“This could be the discovery of the century, depending of course, on far it goes down”

Why?

U.S. Food and Drug Administration

Make No Mistake: Medical Errors Can Be Deadly Serious
The American Hospital Association lists these as some common types of medication errors:
•incomplete patient information
•unavailable drug information
•miscommunication of drug orders, which can involve poor handwriting, confusion between drugs with similar names, misuse of zeroes and decimal points, confusion of metric and other dosing units, and inappropriate abbreviations

example

•Medication errors in US: 44000-98000 deaths/year
•4^th-6^th leading cause of death in US
•3000-6800 are due to medication math errors
•Unit conversion (e.g. grams into milligrams)
•Translation language into equations (e.g. a solution of 50 1-mg drops per liter water into 1 mg/20 ml)
•Unit conversions are also important in many other fields (packaging, architecture, construction etc etc)

What is a meter?

•Early 18^thCentury:
 •Length of pendulum with half length of 1s
•Distance from N-pole to Equator via Paris /10⁷
•1791: second was chosen and 1874 Alloy was made
•1889:more precise by using Platinum/Iridium Alloy
•1960:Using wavelength by using Krypton-86 radiation
•1983: distance traveled by light in vacuum in 1/299792458 s

What is a second?

•Originally 1/86400 of a mean solar day
•1960: based on a tropical year
•1967: 9192631770 periods of radiation corresponding to the transition between two hyperfine states of the ground state of 133Cesium
 

What is a kilogram?

•End of 18^th century: 1 dm³of water
•1889: defined to a Platinum-Iridium weight

Système Internationale (SI)

7 Standard Units: We will use them!!

Quantity	Name	unit
length	meter	m
mass	kilogram	kg
time	second	s
electrical Current	Ampere	A
temperature	Kelvin	k
amount of substance	mole	mol
Luminous intensity	candela	cd

Examples:
Speed: m/s
Acceleration: m/s²
Force: kg·m/s²(N)

Dimensional Analysis

Dimension should be treated as algebraic quantities!

x = x₀ + (at²)/2

Correct dimensionally?

[m]=[m]+([m]/[s]²)[s]²… YES!

Think about unit conversions!
X,X₀in ft. a in m/s²
[ft]=[ft]+([m]/[s]²)[s]²… ????

1 m = 3.281 ft

[ft]=[ft]+([ft]/[s]²)[s]²… YES!

GOOD WAY TO CHECK IN EXAMS & LIFE!!

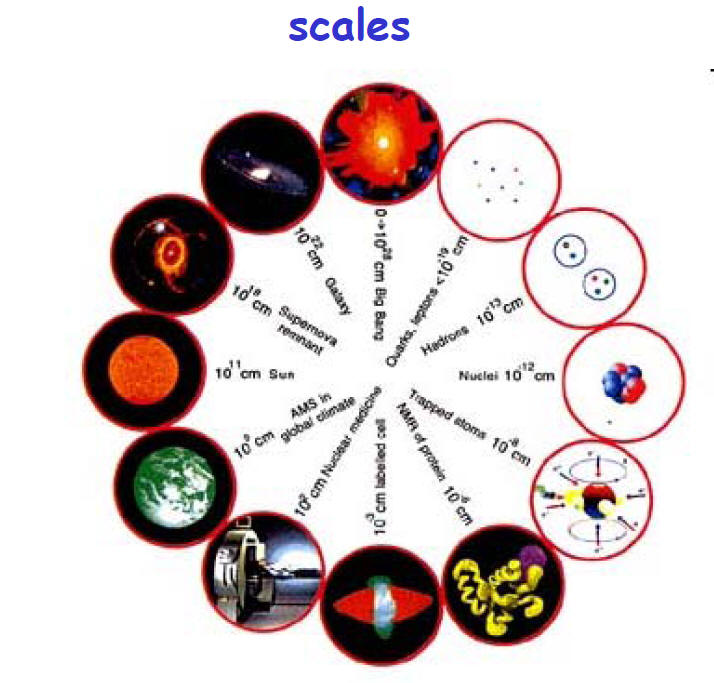
Very large & very small numbers

0.000000000000001=10^-15=1E-15 femto (f)
0.000000000001=10^-12=1E-12 pico (p)
0.000000001=10^-9=1E-9 nano (n)
0.000001=10^-6=1E-6 micro (μ)
0.001=10^-3=1E-3 milli (m)
0.01=10^-2=1E-2 centi (c)
0.1=10^-1=1E-1 deci (d)
1=10⁰=1E+0
10=10¹=1E+1 deca (da)
100=10²=1E+2 hecto (h)
1000=10³=1E+3 kilo (k)
1000000=10⁶=1E+6 mega (M)
1000000000=10⁹=1E+9 giga (G)
10000000000=10¹²=1E+12 tera (T)

Uncertainty & Significance

1.2411 trillion digits known!!

π=3.1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 8214808651 3282306647 0938446095 5058223172 5359408128 4811174502 8410270193 8521105559 6446229489 5493038196...

Significance & Uncertainty

Circumference=2πR=2·3.1415926... ·4.2 =

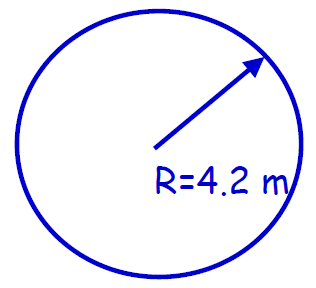
Calculator: 26.38937… m

Right answer: 26 m.

4.2 means that the true value lies
between 4.1 and 4.3:
2π4.1=25.761…=26 m
2π4.3=27.0176…=27 m
so: Right Answer with error: 26±1

The number of significant figures for a result of a division or multiplication is the least accurate of the quantities being divided or multiplied.
 

Significance & Uncertainty

For addition and subtraction the number of decimal places should be equal to the smallest number of decimal places of any term in the sum:

3.0001 + 0.0025 = 3.0026

NUMBER OF DECIMAL PLACES IS NOT THE SAME AS THE NUMBER OF SIGNIFICANT FIGURES!

0.0025: 2 significant figures 4 decimal places
Scientific notation. For example 7·10⁷or 7E+07

2D Geometrical objects

object	surface	circumference
	Length2	4xlength
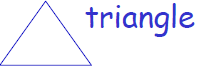	½ x base x height	Side1+side2+side3
	πx radius2 Radius=diameter/2	2 x π x radius
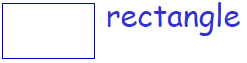	Length x height	2xlength + 2xheight
	πxr1xr2	-

3D geometrical objects

object	surface	volume
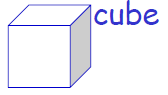	6xlength2	length3
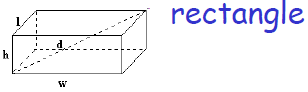	2hw+2lh+2wh	hlw
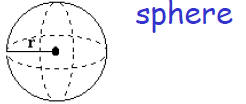	4πr2	4/3 x πr3
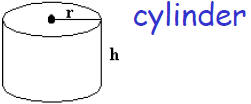	2πrh	πr2h

Coordinate Systems

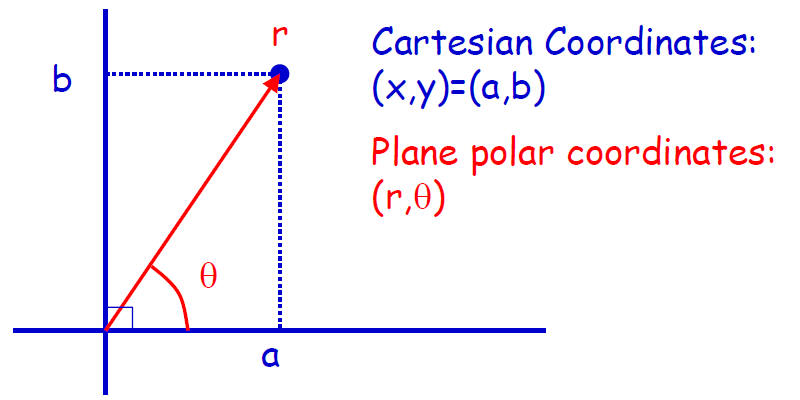
Frame transformation:

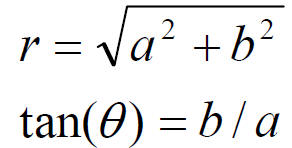
TRIGONOMETRY

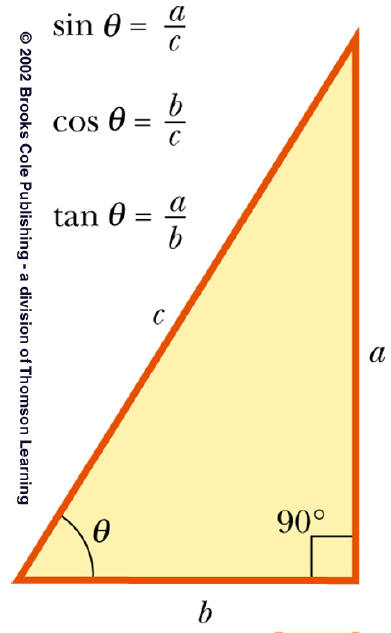
SOH-CAH-TOA:
sin=opposite/hypotenuse
cos=adjacent/hypotenuse
tan=opposite/adjacent

Pythagorean theorem:

c² = a² + b²

Note that sin,cos,tan are dimensionless.

2πradians corresponds to 360o

Be careful…

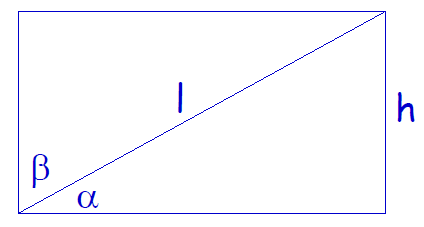
h=l x sinα=l x cosβ
Check carefully which angle is given

Solving quadratic equations

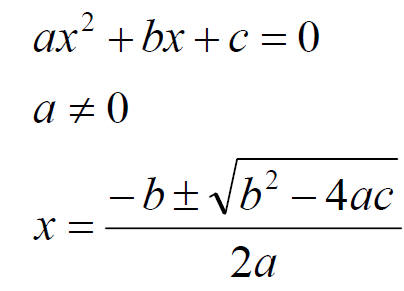
In general there are 2 solutions. In physics problems,
One of them is often not realistic and is thrown out.

How to solve a problem?

There are no general rules but here are some pointers:
1)READ problem carefully!
2)Summarize (throw away unnecessary info)
3)Visualize (drawing can often help)
4)Convert units (consistency)
5)Set up equations:
•Plug in numbers if not comfortable with solving sets of equations
•If confidents, plug in numbers at last moment
6) Check whether answers make sense
7) In exams: once you have solved a problem, check calculations one more time at the end of exam. Especially important if you tend to make small mistakes

Problem:The diameter of the orbit of the earth around the sun is 4x10^11m. (1) What is the distance traveled by the earth in 1 year? (2) in the polar coord. System with the sun in the center, over what angle does the earth travel in 0.30 year?

Calculate the length of the shorter of two sides of a rectangle, which has an area of 24 m²and a perimeter (circumference) of 22 m.

A=lh
C=2l+2h

24=lh so l=24/h
22=2l+2h=2x24/h+2h=48/h+2h
-2h2+22h-48=0

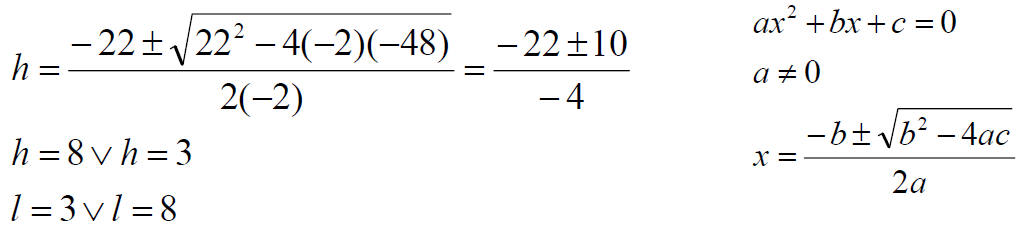
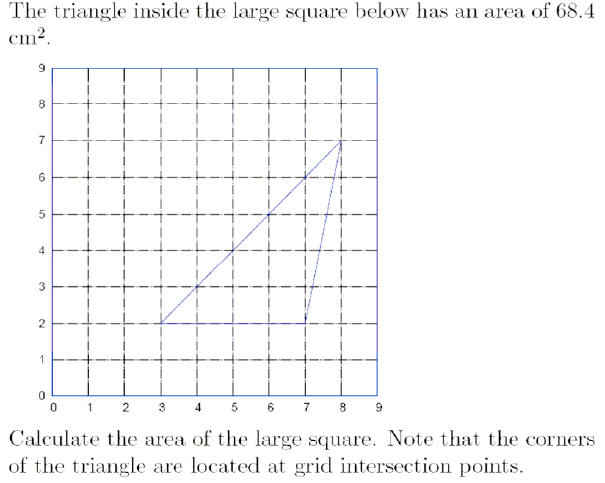
Area of triangle: ½ base x width = ½x4ux5u=10u²
(u: unit of drawing)
10u²=68.4cm²1 u²=6.84cm²
Full square: 9x9u²=81u²corresponds with 81x6.84=554 cm²