Polynomials
Single Variable Polynomials
"I hate variables. Why are you making this so
complicated?" is a question
I hear while listening in on classes teaching polynomials. The answer is
not very difficult: polynomials are complicated. One of the annoying things
about polynomials is that there are a lot of terms that need to be understood
in order to be able to follow the lecture.
Before actually defining a polynomial, lets take a step
back to simple
expressions. If I ask: "What is the coefficient, and what is the variable
in the expression 5x," the perfect class would unanimously respond "the
coefficient is 5 and the variable is x." These are fundamental concepts in
algebra, and the difference between a variable and a coefficient needs to be
fully understood before trying to understand polynomials.
Next, if I write "9, 11, 5, 2, 15" on the board and ask
the class to tell me
what they are in descending order, they would say: "15, 11, 9, 5, 2." This is
because descending means biggest to smallest.
If I were then to ask how many "terms" were in the
expression 5x + 3, I
would hope to get a response of 2. This is the same "terms" as in \combine
like terms." Now, if I write 5x2 + 2x - 3 on the board and ask how many
terms are in this expression, they would hopefully say 3.
Finally, it is time for a definition of a polynomial. A
polynomial in one
variable is an expression of the form:
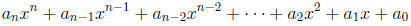
where
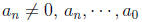 are real numbers, and n is a non-negative integer.
are real numbers, and n is a non-negative integer.
It is time to use some specific terms with respect to this
polynomial.
First, the polynomial above is said to be a polynomial of the variable x (or
a polynomial in x) because x is the variable in the expression. The terms
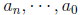 are called the coefficients, with
are called the coefficients, with
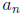 having the special name of
having the special name of
leading coefficient because it is in front, and
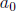 is the constant term
is the constant term
because it is just some real number and does not change. We have written
the expression in descending order with respect to the exponent of x.
Finally, the degree of the polynomial is just the highest power of x. In the
expression above, the degree is n.
Polynomials of Several Variables
Polynomials in several variables are what they sound like
{ polynomials with
more than one variable. What does this look like? This is best explained
with an example:
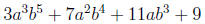
This is a polynomial in two variables, a and b. Like
single-variable polynomials,
these terms have a degree also. However, the degree of a term in a
polynomial in several variables is the sum of the exponents of the variables
in a term. Finally, the degree of the polynomial is the degree of the term
with the highest degree, just like in single-variable polynomials.
Right now, it is enough to know the terminology that goes
with these
polynomials. The leading coefficient is defined the same as it is for polynomials
of one variable. We will leave these now and move on to manipulating
polynomials.
Adding and Subtracting Polynomials
Adding and subtracting polynomials is not very different
than manipulating
any other algebraic expression. We add and subtract plynomials by combining
like terms. Combining like terms involves collecting terms with variables
of the same degree, and then combining them by adding or subtracting them
as indicated. For example, 5x3 and 2x3 are like terms because they have the
same variable and the same exponent. Suppose we have 5x3 - 2x3. We can
rewrite this as 5x3 +(-2)x3. Now, we can use the distributive law in reverse
to write this as (5+(-2))x3. Then, we can perform the operation inside the
parenthases in accordance with the order of operations to get 3x3.
To make this more concrete, a complete example is needed.
Suppose we
want to add two polynomials: x3 +4x2 -1 and 2x4 +3x3 -2x2 +x-3. This
addition would be written as:
(x3 + 4x2 - 1) + (2x4 + 3x3 - 2x2 + x - 3)
Since there is nothing that can be done to simplify the
expressions inside the
parenthases, we can get rid of them. We now have
x3 + 4x2 -1 + 2x4 + 3x3 - 2x2 + x - 3
Now, we can rewrite this long expression (which is a new
polynomial) in
descending order:
2x4 + x3 + 3x3 + 4x2 - 2x2 + x - 1 + (-3)
Now, we use the distributive law in reverse to get
2x4 + (1 + 3)x3 + (4 - 2)x2 + x + ((-1) + (-3))
Evaluating these coe cients yields:
2x4 + 4x3 + 2x2 + x - 4
At this point, we have no more like-terms to combine, so
we are done. So,
this is the sum of the above two polynomials.
Multiplying Polynomials
Multiplication of polynomials can get complicated.
However, it is nothing
more than the distributive property applied many times. The net result is
that every term in the first polynomial is multiplied by every term in the
second polynomial. To see this, we will use an example. Suppose we want to
multiply x3 + 4 and 2x2 + x. We can write this as
(x3 + 4)(2x2 + x)
Now, we can use the distributive law to get:
2x2(x3 + 4) + x(x3 + 4)
Then, we must distribute two more times:
2x2 ∙ x3 + 2x2 ∙ 4 + x ∙ x3 + x ∙ 4
Doing the multiplication gives us:
2x5 + 8x2 + x4 + 4x
Since there are no like terms to combine, we fininsh by
writing this in descending
order:
2x5 + x4 + 8x2 + 4x
Now, a little more complicated example is:
(x3 + 2x2 - x - 1)(x - 1)
We have to distribute.
x(x3 + 2x2 - x - 1) + (-1)(x3 + 2x2 - x - 1)
Doing the two distributions, we get:
(x4 + 2x3 - x2 - x) + ((-1)x3 + (-2)x2 + x + 1)
Next, we write this in descending order:
x4 + 2x3 - x3 + (-1)x2 - 2x2 - x + x + 1
Our next task is to undo the distribution of the coefficients for like terms:
x4 + (2 - 1)x3 + ((-1) + (-2))x2 + ((-1) + 1)x + 1
Doing the additions inside of the parenthases yields
x4 + 2x3 + (-3)x2 + 0x + 1
Which is equivalent to
x4 + 2x3 - 3x2 + 1
And we are done!


