The Polynom Package
Abstract
The polynom package implements macros for manipulating polynomials,
for example it can typeset long polynomial divisions. Such long divisions can
be shown step by step. The main test case and application is the polynomial
ring in one variable with rational coefficients.
1 Introduction
Donald Arseneau has contributed a lot of packages to the
 community. In
community. In
particular, he posted macros for long division on comp. text. tex , which were
also published in the TUGboat [1]. With these definitions, one could just write
\longdiv{12345}{13} to get the long division shown in Figure 1 (a). In fact,
that
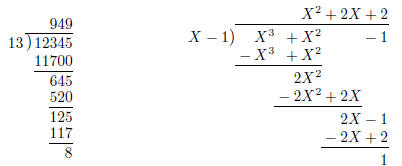 |
|
| (a) \longdiv{12345}{13} | (b) \polylongdiv {X^3+X^2-1}{X-1} |
| Figure 1: Integer and polynomial long division | |
integer long division has been typeset using the code from
the location cited. The
polynom package allows to do the similar job with polynomials, see Figure 1 (b).
Figure 2 shows partial long divisions.
An application of polynomial division is shown in Figure 3: the Euclidean
algorithm to determine a greatest common divisor of two polynomials. Note that
in the case here, a greatest common divisor is uniquely determined up to a
scalar
factor, so X - 1 and 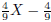 are both greatest
common divisors in the example.
are both greatest
common divisors in the example.
| \polylongdiv [stage=1] {(X-1)(X^2+2X+2)+1}{X-1} |
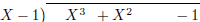 |
| \polylongdiv [stage=2] {(X-1)(X^2+2X+2)+1}{X-1} |
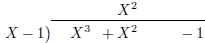 |
| \polylongdiv [stage=3] {(X-1)(X^2+2X+2)+1}{X-1} |
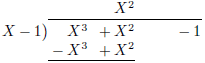 |
| \polylongdiv [stage=4] {(X-1)(X^2+2X+2)+1}{X-1} |
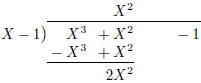 |
 |
|
Figure 2: Stepwise polynomial long division. The whole
division is shown with
stage=10. Note that other printing styles, see table 7, might require one more
stage to put the remainder next to the result
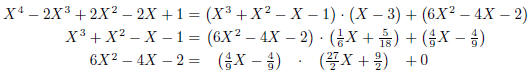
\polylonggcd {(X-1)(X-1)(X^2+1)} {(X-1)(X+1)(X+1)}
Figure 3: Euclidean algorithm with polynomials; the last nonzero remainder is a
greatest common divisor
\polyfactorize {(X-1)(X-1)(X^2+1)}
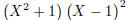
\polyfactorize {2X^3+X^2-7X+3}
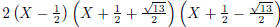
\polyfactorize {120X^5-274X^4+225X^3-85X^2+15X-1}
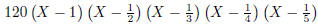
Figure 4: Factorizations of some polynomials
2 Commands
The tables 5 and 6 list the user commands defined by this package. Each
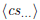
stands either for a
![]() control sequence to
store the internal representation of the
control sequence to
store the internal representation of the
result, or it stands for a previously saved result to operate with. The
polynomials
<a> and <b> are 'verbatim' polynomials as you would type them in math mode:
you may use +, -, *, \cdot, /, \frac, (, ), natural numbers, symbols like e,
\pi,
\chi, \lambda, and variables; the power operator ^ with integer exponents can be
used on symbols, variables, and parenthesized expressions. Never use variables
in
a nominator, denominator or divisor.
| print long division a/b (maybe partially) |
\polylongdiv 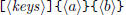 \polylongdiv 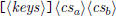 |
| print Euclidean algorithm for gcd(a, b) |
\polylonggcd 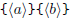 \polylonggcd 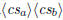 |
| print factorization of the polynomial a |
\polyfactorize 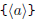 \polyfactorize 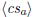 |
Table 5: High-level user commands. The optional argument
of the \polylongdiv
command changes settings for the particular division
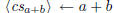 |
\polyadd 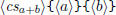 \polyadd 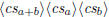 |
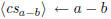 |
\polysub 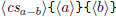 \polysub 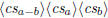 |
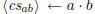 |
\polymul 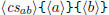 \polymul 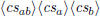 |
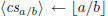 \polyremainder ←a mod b |
\polydiv 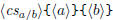 \polydiv 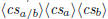 |
 |
\polygcd 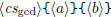 \polygcd 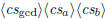 |
| print polynomial a | \polyprint 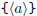 \polyprint 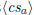 |
Table 6: Low-level user commands
Note, however, that the support of symbols is very limited and that there is
neither support of functions like sin(x) or exp(x), nor of roots or exponents
other
than integers, for example π or ex. For teaching purposes this shouldn't be
a
major drawback. Particularly because there is a simple workaround in some cases:
the package doesn't look at symbols closely, so define the
function or 'composed
symbol' like 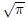 as a symbol. For example, you could write
as a symbol. For example, you could write
\newcommand\epowerx{e^x}
\[\polylongdiv{\epowerx x^3-\epowerx x^2+\epowerx x-\epowerx}{x-1}\]
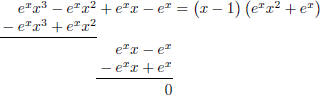
Here the quotient and remainder are written next to
dividend and divisor. This
'style=B-feature' is discussed in the next section.
Let's conclude this section with an example of the low-level commands. If we
want to divide 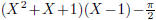 by X-1 and print quotient and remainder,
by X-1 and print quotient and remainder,
we could do it like this:
\polydiv\polya {(X^2+X+1)(X-1)-\frac\pi2} {X-1}
'The quotient is \polyprint\polya,
the remainder \polyprint\polyremainder.'
Of course, we all know the result, so it isn't shown here. The calculation alone
could also be done by, for example,
\polymul\polya {X^2+X+1} {X-1}
\polysub\polya \polya {\frac{\pi}{2}}
\polydiv\polya \polya {X-1}
3 Keys
\polyset Predefined variables are X and x, the default style for printing long
division is
shown in Figure 1 (b), and the left and right delimiters are \left( and \right).
The macro \polyset changes such default settings and accepts a comma separated
list of 'key=value' pairs. This is implemented using the keyval package [3].
Possible
keys and values are given in table 7. To make the style selection C clear and to
use
variables and delimiters other than the default, look at the output of the
following
example.
\begin{center}
\polyset{
vars=XYZ\xi, % make X, Y, Z, and \xi into variables
style=C, % use nonstandard style
delims={[}{]}}% nongrowing brackets
\polylongdiv{(\xi-1)(\xi^2+2\xi+2)+1}{\xi-1}
\end{center}
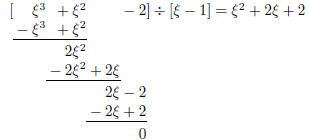
Afterwards previous settings are restored since the
changes are made inside the
center environment or, more generally, inside a group. The same \polylongdiv
command now makes no sense. A constant would be divided by a constant.
| vars=<token string> | make each token a variable |
| style=<AlBlC> | define style for long division |
| div=<token> | define division sign for style=C, default is ÷ |
| stage=<number> | print long division up to stage <number> (starting with 1) |
| elims={<left >}{<right>} | define delimiters used for parenthesized expressions |
Table 7: Keys and values. The delims key has in fact an
optional argument for
use with growing delimiters. In this case you must specify invisible versions of
the
two delimiters. The default is delims=[{ \left.}{ \right.}]{ \left(}{ \right)}


