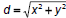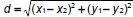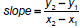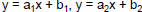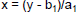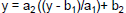Algebra The Easy Way – Chapter 9
Graphing Skills |
Objectives
• Distance between two points
• Graphing solutions to equations
• Calculating the slope of a line
• Graphing inequalities and curves
• Graphing relationships |
| Graphing Data, and Finding Distances
• Good overview at the start of chapter - based on
compass
direction
– Two dimensions: North -> up, East -> to the right
– Origin at 0 East, 0 North (bottom left corner)
• Label a point in space using an ordered pair (x, y), with x
representing the East distance, and y the North
– By convention, x always stated first
– The x and y in a point (x, y) are called a coordinates
• Important task: find distance from origin to a point, or
between two points
– General formulas: from origin: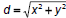
– Between two points: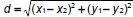 |
| Graphing Equation Solutions
• Observation: nice connection between functions
(example:
y=f(x)) and graphs, if we change
– North -> y, East -> x (call these “x and y axes”)
– Origin at (0,0)
• Solutions to a function like y=2x can be plotted as points
– (1,2), (2,4), (3,6), (4,8), etc. (Fig. 9-11)
– Set of points representing solutions: graph of equation
– Negative numbers legal too: extend axes (Fig. 9-16)
• Figs. 9-17 - 9-19 show a number of other examples
– All go through the origin, and represent y = f(x)
– General form of linear function: y = f(x) = ax + b
• Two points required to uniquely determine a line |
| The Slope of a Line
• Slope: angle of a graph relative to horizontal
– Can be positive, zero, or negative (Fig. 9-26)
– Calculating slope (Fig. 9-27):
• Pick two points (x1,y1), (x2,y2)
• Calculate distance up (along y axis)
• Divide by distance sideways (along x axis)
• General formula (works for negative slopes):
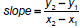
– For equations of the form y = mx + b, all equations with the
same “m” have the same slope
• If m < 0, slope is negative
• The “b” represents the y-intercept: point at which the graph
crosses the y axis
• Set y=0 to find x-intercept, x=0 to find y-intercept (p. 126) |
| Graphing Inequalities
• Often useful to graph inequalities, e.g. x + y ≤ 10
– Assume x, y ≥ 0
– Fig. 9-30 shows integer values that make the equation true
(sum of x and y is ≤ 10)
– If we draw a line along the boundary, points below make
the equation true, points above make it false
• More on this subject later
• So for an equation ax + by ≤ c (or ≥ c) we draw the line
ax + by = c
– All points on one side make the inequality true; all points
on the other make it false |
| Graphing Curves, other Functions
• Many equations cannot be drawn using a straight
line
– Example: y = x2(see Fig. 9-34, 9-35, 9-36)
– Also called a nonlinear (“not a line”) equation
– Note the effect shown in Fig. 9-35 of a multiplier--changes
the shape (steepness) of the curve
• Functions may also be discontinuous: points on the line
are not joined by a smooth curve (Fig. 9-37)
– Simple continuity test: function can be drawn without lifting
your pencil from the paper
• Most business data can be massaged into graphical
format, and the old adage of a picture being worth a
thousand words will often hold true |
| Displaying Graphical Relationships
• Book discusses several examples of using graphs to
highlight correlations between data elements
– Temperature and gas volume
– Rainfall and visits to a park
• Note negative slope in Fig. 9-39: visits decrease as rainfall
increases
– Important to distinguish independent (x) variable from
dependent (y) variable
• Example in Fig. 9-40 shows an incorrect comparison
– Hamburgers and library books (?)
– Turns out another variable (population) is the real independent
variable
• Be careful to avoid this problem |
Algebra The Easy Way – Chapter 10
Systems of Two Equations |
| Objectives • Goal:
find solution to a set of two equations
• Graphical representation of solution
• Simultaneous equation solution methods
– Substitution method
– Elimination method
• General formulas for solutions |
| Catching the Culprit
• Problem from book: catching the “culprit”
– Detective starts at position 2, moves at speed 4
• y = f(x) = 2 + 4x
– Culprit starts at position 10, moves at speed 3
• y = g(x) = 10 + 3x
– Both start at the same instant
– When will their paths cross?
• Initial insight: the two functions can be graphed
simultaneously (Fig. 10-4)
– Crossing point shows when the culprit will be caught
– Looks like at position 34 (right at the river)
– How long will the chase take (what is value of x)? |
| Solving Simultaneous Equations
• Since both equations are a function of x, we can
set them
equal to each other, then solve for x:
2 + 4x = 10 + 3x
2 + 4x - 3x = 10 + 3x - 3x (Subtract 3x from both sides)
2 + x = 10
2 - 2 + x = 10 - 2 (Subtract 2 from both sides)
x = 8
• Now plug solution for x back into either equation:
y = f(x) = 2 + 4(8)
y = 34
• So graphical solution was correct |
| Another Example: Supply & Demand
• Quantity supplied, demanded is a function of price
p
– Supply: q = f(p) = -5 + 30p
• Suppliers will supply more as price increases (positive slope)
– Demand: q = g(p) = 200 - 15p
• Consumers will demand less as price increases (negative slope)
• Solving for p, we get
p = 4.556, q = 131.7
• Graph of solution in Fig. 10-5
• Key assumption in this “economy”: other things equal
– More on this later… |
| Equation Substitution
• Solve for one variable or the other, then
substitute into the
other equation
– If we have 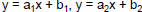
– Solving for x in the first equation we get
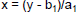
– Then plug that value for x into the second:
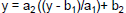
– We’ll do the example at the bottom of P. 151
• General process (algorithm):
– Use one equation to find y in terms of x (or x in terms of y)
• Experience determines which to substitute for the other
– Substitute for y in the other equation
– Solve for x (or y)
– Insert result into first equation to determine value of y (or x) |
| The Elimination Method
• For a pair of equations with two unknowns:
4x + 3y = 38
6x - 3y = 12
– We can add the two equations together
(4x + 6x) + (3y - 3y) = 38 + 12
– Conveniently, the y term “drops out”: we can solve for x
– No violation of “golden rule”: two sides of second equation are
equal, so we are adding the “same thing” to both sides
• Tricky part: getting the coefficients to match so one drops out
• Can also subtract one equation from the other if all
coefficients are positive |
| The Elimination Method: Algorithm
• Two equations, with two unknowns (x, y)
1. Make coefficients of x or y match, usually by multiplying. It is
legal to multiply the two equations by different numbers
2. Subtract the two equations from each other (left-hand side
from left-hand side, right-hand side from right-hand side)
3. Result will be a new equation with one variable eliminated:
solve for the other variable
4. Plug the result into either of the original equations and solve
for the other variable
• In step 1, may also set things up so coefficients are
negatives of each other--then add in step 2 |
| Notes on Systems of Two Equations
• General formulas for elimination, substitution
methods are
given on p. 156
– Not useful for real-world problems, but nice to know they exist
• Both methods are useful, and only experience will help
decide which is better for a given problem
• Equation system will have no solutions when the two
equations are parallel lines
• Equation system will have an infinite number of solutions of
the two equations define the same line (example p. 158)
– Not always obvious this is the case |