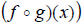Operations and Functions
1.4 Operations and Functions
Let f(x) be a function with domain A.
Let g(x) be a function with domain B.
Methods for combining functions:
1. Sum ( f + g)(x) = f (x) + g(x) (domain of f + g is A∩ B )
2. Difference ( f - g)(x) = f (x) - g(x) (domain of f - g is A∩ B )
3. Product ( fg)(x) = f (x)g(x) (domain of fg is A∩ B )
4. Quotient
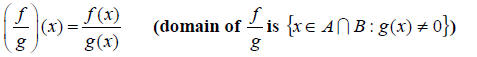
5. Composition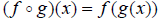 
(domain we will discuss later in this section)
Example 1: Let f (x) = 2x^2 - 3x +1 and let g(x) =
5x - 3 . Find and state the domain of the
following functions:
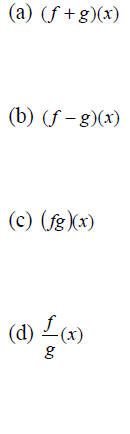
Example 2: Let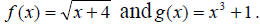 
Find:
(d) the domain of f/g.
Composition of Functions:
There is one more type of function combination we will
see, it is called the
COMPOSITION of two functions and is denoted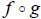 
.
By definition: (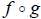
)(x) = f (g(x)) This is often
read as “f of g of x”. What you do to
evaluate this composition function at a number x is evaluate g at x, then plug
that number
into f.
Example 3: Let f (x) = x^2 + x -1 and g(x) = 1- 2x . Find:
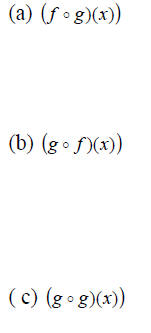
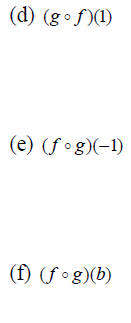
The domain of 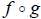is
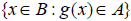or To find the domain of
, first compose the
functions and find the rule for f (g(x)) . Then find the domain of this new
function
f(g(x)) . Also find the domain of g(x) (the “inside” function). Combine these
and you
will have the domain of .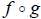
Example 4: Let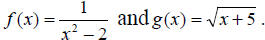 
Find:
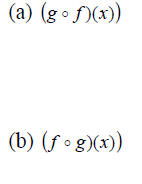
(c) The domain of 