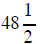More Tutorials

Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Dividing Polynomials

Example 3 using a 0x as a place holder for a missing term

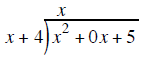divide the first term of the binomial outside into the first term inside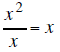

and put the results above the division bar

multiply the x on top by the x + 4 outside and write the product of x( x + 4) under the trinominal

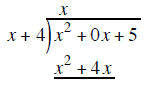
multiply EACH term in the new row by −1 to create a subtraction problem

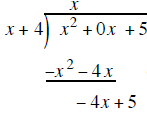combine the terms above the underline and bring down the + 5

Start the process over again with the − 4 x + 5 term and the x + 4 outside

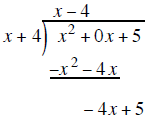divide the first term of the binomial outside into the first term of − 4 x +1

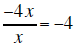
multiply the − 4 on top by the x + 4 outside − 4(x + 4) and write the product under the − 4 x + 5

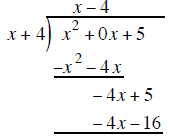
multiply EACH term in the new row by −1 to create a subtraction problem

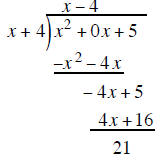combine the terms above the underline

we are done and have a remainer of 21

the answer is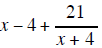

Example 4

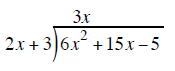divide the first term of the binomial outside into the first term inside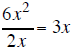

and put the results above the division bar

multiply the x on top by the 2x + 3 outside and write the product of 3x(2x + 3) under the trinominal

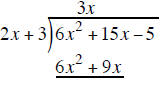
multiply EACH term in the new row by −1 to create a subtraction problem

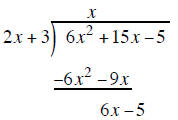combine the terms above the underline and bring down the − 5

Start the process over again with the 6x − 5 term and the 2x + 3 outside

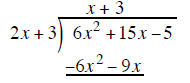
divide the first term of the binomial outside into the first term of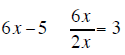

multiply the 3 on top by the 2x + 3 outside 3(2x + 3) and write the product under the 6x −5

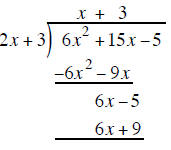
multiply EACH term in the new row by −1 to create a subtraction problem

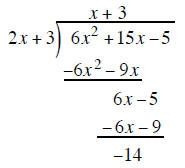combine the terms above the underline

we are done and have a remainer of −14

the answer is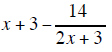

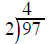divide the 2 outside into the first number inside and put the results over the 9

multiply the 4 on top by the 2 outside and write the product 8 under the 9

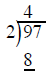multiply the 8 in the new row by −1 to create a subtraction problem

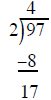combine the terms above the underline and bring down the 7

Start the process over again

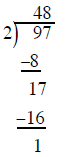
the answer is