Concepts of Secondary School Mathematics

Why Math 486?

Although this is a course for potential high school teachers, it is not the goal of this class to teach you how
to teach. Instead, we are trying to obtain an insight into mathematical motivations, how to structure and
communicate mathematical arguments, and how to explore the concepts underlying the material that you will
be teaching.

For example: suppose someone tells you that

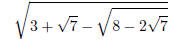
is a rational number. What method would you use to solve for this rational number algebraically? Is there
another method? How would you find other examples of the same type?

Another example: You may know that fractions can be converted into decimals that either terminate or
eventually repeat. Did you know that the block of repeating numbers can be no bigger than the denominator
of the fraction? Why is this true? Is there a good explanation for this? Could we find the possible sizes of
the blocks for a given denominator?

Or consider the following problem, from a math contest: prove that any nonnegative polynomial can be
written as the sum of squares of polynomials. How would you approach solving this problem? What techniques
and theorems might be useful to attack this question? What would be the best way of communicating
your solution?

In this class, we will have the opportunity to use concepts such as number systems, divisibility rules, and
polynomials in deeper and more creative ways than you may have previously.

Overview of material

Students should read Chapter 1 of the text on their own as soon as possible. This will provide an introduction
to the ideas and approach of this class. Chapters 2 and 3 cover real numbers and functions. Chapter
4 discusses techniques in equation-solving. If time permits, we will cover some of Section 4.2 and 4.3.
Chapters 5 and 6 cover some number systems. We will cover most of the material in these two chapters.

Course policies

•Cell phones, pagers, etc., are to be turned o during class.
•Unless otherwise stated, all answers on assignments and exams must be justified. A correct answer
with no justification will earn minimal partial credit.
•You are allowed and encouraged to work with others on the problem sets, but you must structure the
write-up and do the final writing of your solutions on your own.
•Calculators are not allowed on the exams.
•Late homeworks will not be accepted.
•Make-up exams will not be given.
•You must notify me of any conflict with an exam at least one week in advance of the scheduled time.
•Travel arrangements are not a sufficient excuse. (Don't buy a plane ticket yet for finals week.)
•You are held to the standards of ethics of the university.

Required text
Mathematics for High School Teachers: An Advanced Perspective, Z. Usiskin et al.

Grading
You are guaranteed an A (possibly ) for a score of 90% or higher, a B (possibly ) for a score of 80% or
higher, etc. It is likely that these thresholds will be lowered (but not raised) at the end of the course.

Problem Sets and Proof Revisions: 10%
First exam: 20%
Second exam: 30%
Final exam: 40%

As one of the goals of the course is an improved grasp of mathematical argumentation, there will be approximately four Proof Revisions: assignments which will involve multiple revisions and oral presentations.

Exams
The two midterms will be held in class on February 5 and March 17. The date and location for the final
exam will be announced.