Key Concepts in Linear Algebra
I. Notation s: Vectors and Vector Spaces
• n-dimensional vector: Ordered n-tuple
• Notation:
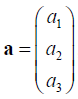
where
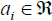(real-valued elements) is a 3-dim column vector. A row vector is denoted by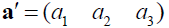
• Vector Space: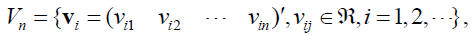
•
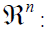n-dimensional
Euclidean space
• ith elementary vector :
•
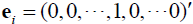
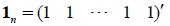
II. Linear independence, linearly independent vectors, basis of a vector
space,
subspaces, dimension (rank) of a vector space, space spanned by a collection
of vectors
III. Inner (dot) Product of two vectors
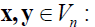
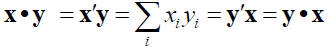
• Other notations:
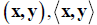
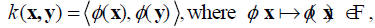the
feature space.
• Length of a vector, vector norm
• Angle between two vectors,
• Mutually orthogonal vectors,
• Pythagoras’ theorem, Triangle inequality, Cauchy-Schwartz
inequality,
• Orthogonal basis, orthonormal basis.
• Coordinates of a vector in terms of an o.n.b.
• Gram-Schmidt process for forming an o.n.b., Extension of an o.n.b.
for a subspace V to an o.n.b. for the space Vn .
• Orthogonal Complement of a vector space
IV. Matrices (definition, sums and products, transpose
• Rank of a matrix
• Space spanned by columns of a matrix A,
• Null space of a matrix,
• Matrix norm
V. Trace, Determinant, Eigen–values and Eigen-vectors and their properties, Spectral decomposition of a real symmetric matrix A.
VI. Singular Value Decomposition of a matrix A (SVD).
VII. Simultaneous diagonalization of two matrices
VIII. Symmetric and Idempotent matrices, Partitioned matrices.
IX. Linear forms, Quadratic forms, Positive semi-definite (p.s.d) (n.n.d.), Positive Definite (p.d.).
X. Systems of Linear Equations (Solution space), generalized inverse of a matrix, computation of a g-inverse, Moore-Penrose inverse of a matrix.