Solving Exponential and Logarithmic Equations

I. Review of Some Key Properties of Exponential and Logarithmic Functions

A. Base-Exponent Property

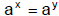if and only if x = y

B. Inverse Properties
Exponential functions and logarithmic functions are inverses which undo one another.

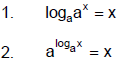
C. Change of Base Formula

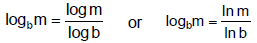
D. Property of Logarithmic Equality

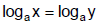if and only if x = y.

E. Product Rule of Logarithms

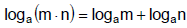
F. Quotient Rule of Logarithms

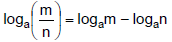
G. Power Rule of Logarithms

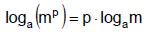
II. Exponential Equations

A. Definition
Equations with variables in the exponents are called exponential equations.
Examples:

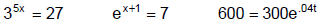
B. Strategies for Solving Exponential Equations
Method 1: Get the Same Base
Rewrite each side of the equation as a power of the same base and then apply the
Base-Exponent Property to solve for the variable. To check, plug your un-rounded
solution into the original equation and see if it works.

Example 1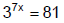

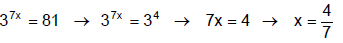
Check:

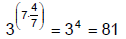
Method 2: Using 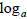to undo
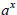
Isolate the exponential expression. Take the log base a of both sides. Use the inverse
property to simplify one side and, if necessary, the change of base formula to simplify
the other. Solve for the variable. To check, plug your un-rounded solution into the
original equation and see if it works.

Example 2

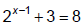
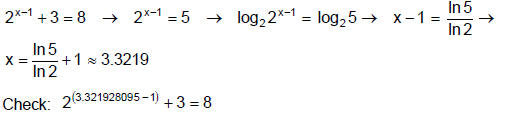
Method 3: Using ln and the Power Rule to undo
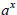
Isolate the exponential expression. Take the natural log of both sides. Use the power
rule of logarithms to make the exponent a coefficient. Solve for the variable. To check,
plug your un-rounded solution into the original equation and see if it works.

Example 3

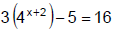
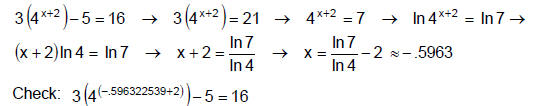
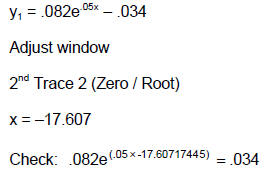
Method 4: Graphical Solution
Put the equation in standard form (everything on the left side of the equal sign and zero
on the right). Let the left side equal 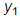. Adjust the window. Use the Zero / Root
feature to find the zeros.

Example 4

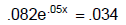
III. Logarithmic Equations

A. Definition
Equations containing variables in logarithmic expressions are called logarithmic equations.
Examples:

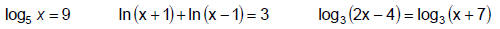
B. Strategies for Solving Logarithmic Equations
Method 1: Using the Definition of a Logarithm

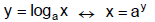
Use the properties of logarithms to write the equation so there is no more than one log
on each side. Use the definition of a log to rewrite the equation in exponential form.
Solve for the variable. To check, plug your un-rounded solution into the original
equation and see if it works. You may have to use the change of base formula.

Example 5

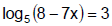
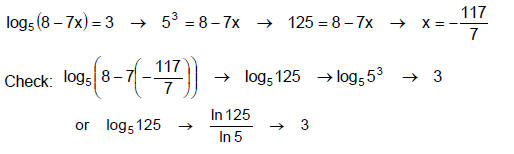
Method 2: Exponentiating Both Sides
Use the properties of logarithms to write the equation so there is no more than one log on
each side. Exponentiate both sides using base a. Simplify one side using the inverse
property to solve for the variable. To check, plug your un-rounded solution into the original
equation and see if it works. You may have to use the change of base formula.
NOTE: It is especially important to check your solutions if you end up with a quadratic.

Example 6

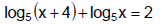
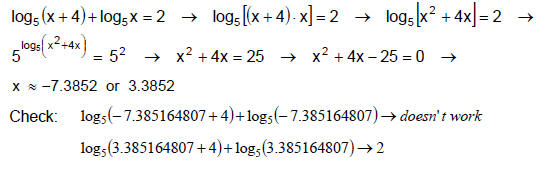
Method 3: Graphical Solution
Put the equation in standard form (everything on the left side of the equal sign and zero
on the right). Let the left side equal y₁. If the logs are not base 10 or base e, use the
change of base formula to rewrite the logs. Adjust the window. Use the Zero / Root
feature to find the zeros.

Example 7 2ln(x–5.1) =8.9